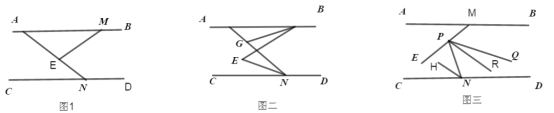
【题目】(1)如图1,![]() ,
,![]() 分别在
分别在![]() 上,试说明∠MEN=∠INC+∠IME.
上,试说明∠MEN=∠INC+∠IME.
(2)如图2,在(1)的条件下,若![]() 平分
平分![]() ,在
,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,使
,使![]() 恰好平分
恰好平分![]() ,
,![]() ,且
,且![]() 的补角比
的补角比![]() 的3倍多
的3倍多![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在问题(1)(2)的条件下,若点![]() 是
是![]() 上一动点(不包含点
上一动点(不包含点![]() 和点
和点![]() ),连接
),连接![]() .
.![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,过
,过![]() 作
作![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,下列结论:①
上运动时,下列结论:①![]() 的值不变;②
的值不变;②![]() 的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
参考答案:
【答案】(1)见解析;(2)40°;(3)②正确,证明见解析
【解析】
(1)在△IEM中,利用外角∠MEN=∠NIM+∠IME推导得到;
(2)先求出∠CNF的值,进而得到∠NFM,然后利用∠FNC与∠MGN的关系得到∠MGN的大小,最后在△FGM中得出∠FMG的大小,进而得出∠FME;
(3)求出∠RPQ=∠4-∠NPR=∠4―∠1,然后在△PKN中,利用内角和180°可算出∠RPQ为定值.
(1)∵AB∥CD
∴∠MIN=∠INC
∵∠MEN=∠MIN+∠IME
∴∠MEN=∠INC+∠IME;
(2)∵∠ENC=19°,EN平分∠FNC
∴∠FNC=38°=∠MFN
∵![]() 的补角比
的补角比![]() 的3倍多
的3倍多![]()
∴180°-∠MGN=3×38°+8°
∴∠MGN=58°
∴AMG=∠MGN-∠MFN=20°
∴∠AME=40°;
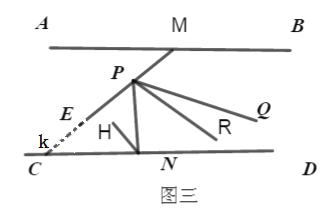
(3)如下图,延长ME交CD于点K,设∠HNP为∠1,∠HNK为∠2,∠MPQ为∠3,∠QPN为∠4
∵AB∥CD
∴∠AME=∠MKN=40°
∵PQ平分∠MPN,NH平分∠PNC
∴∠1=∠2,∠3=∠4
∵PR∥NH
∴∠1=∠NPR
∴∠RPQ=∠4-∠NPR=∠4―∠1
在△PKN中,∠1+∠2+180°-∠3-∠4+40°=180°
∴2(∠4-∠1)=40°
∴∠4-∠1=20°
∴∠RPQ=20°不变,②正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题:
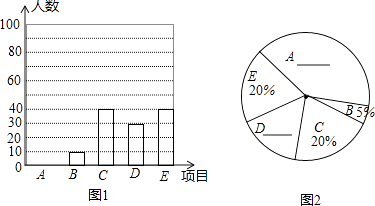
(1)在这项调查中,共调查了名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人? -
科目: 来源: 题型:
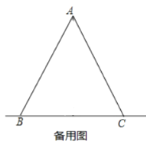
查看答案和解析>>【题目】如图,在
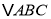 中,
中,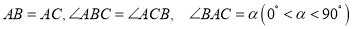 ,
,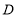 为直线
为直线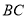 上一动点(不与点
上一动点(不与点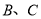 重合),在
重合),在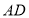 的右侧作
的右侧作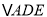 ,使得
,使得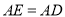 ,
,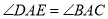 ,连接
,连接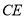 .
.(1)当点
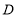 在线段
在线段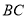 上时,求证:
上时,求证: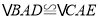 ;
;(2)当
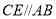 时,若点
时,若点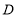 在线段
在线段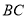 上,
上,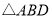 中最小角为
中最小角为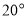 ,请求出
,请求出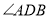 的度数;
的度数;(3)在点
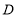 的运动过程中,当
的运动过程中,当 垂直于
垂直于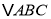 的某边时,求
的某边时,求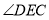 的度数(用含
的度数(用含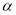 的代数式表示).
的代数式表示).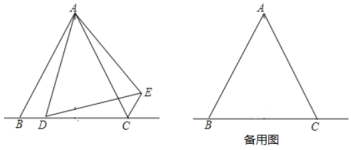
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量
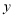 (升)与行驶时间
(升)与行驶时间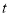 (小时)的关系如下表,请根据表格回答下列问题:
(小时)的关系如下表,请根据表格回答下列问题:时间/小时
0
1
2
3
4
5
邮箱剩余油量/升
50
45
40
35
30
25
(1)汽车行驶前油箱里有_____________升汽油,汽车每小时耗油____________升;
(2)请写出
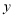 与
与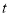 的关系式;
的关系式;(3)当汽车行驶24小时时,油箱中还剩余多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或
C.1或
D. 或
或 
-
科目: 来源: 题型:
查看答案和解析>>【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
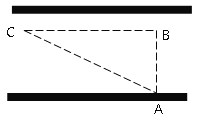
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
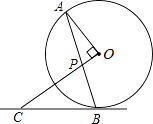
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为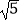 ,OP=1,求BC的长.
,OP=1,求BC的长.
相关试题

