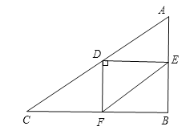
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 运动的时间是
运动的时间是![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 连结
连结![]()

(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值,如果不能,说明理由;
值,如果不能,说明理由;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)能,![]() ;(3)
;(3)![]() 或
或![]() .理由见解析.
.理由见解析.
【解析】
(1)根据30°所对的直角边是斜边的一半即可求出![]() ,从而证出结论;
,从而证出结论;
(2)根据平行四边形的判定定理可证四边形![]() 是平行四边形,然后根据菱形的定义可得当
是平行四边形,然后根据菱形的定义可得当![]() 时,四边形
时,四边形![]() 是菱形,然后列出方程即可求出结论;
是菱形,然后列出方程即可求出结论;
(3)根据直角三角形的直角分类讨论,分别画出对应的图形,根据平行四边形的性质、30°所对的直角边是斜边的一半即可分别求出结论.
![]() 证明:
证明:![]()
![]()
在![]() 中,
中,![]() ,
,
![]()
又![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
当![]() 时,四边形
时,四边形![]() 是菱形,
是菱形,
![]() ,
,
解得![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 能够成为菱形.
能够成为菱形.
![]() 解:①当
解:①当![]() 时,
时,![]()
![]()
![]()
![]()
解得![]() .
.
②当![]() 时,
时,

![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
![]() 是直角三角形.
是直角三角形.
![]() ,
,
![]()
![]()
![]()
解得![]() ;
;
③当∠DFE=90°时,此时点E和点B重合,但![]() ,点E与点B不重合,故此种情况不存在.
,点E与点B不重合,故此种情况不存在.
综上所述:![]() 或
或![]() .
.
![]() 当
当![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.

(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,格点三角形
 (顶点为网格线的交点)的顶点
(顶点为网格线的交点)的顶点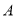 ,
,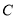 的坐标分别为
的坐标分别为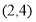 ,
,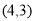 .
.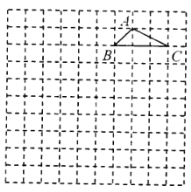
(1)请在网格图中建立平面直角坐标系;
(2)将
 先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的
先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的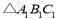 ,并直接写出点
,并直接写出点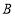 的对应点
的对应点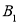 的坐标;
的坐标;(3)若
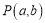 是
是 内一点,直接写出
内一点,直接写出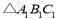 中的对应点
中的对应点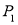 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:

(1)填空:样本容量为________,
 ________;
________;(2)把频数分布直方图补充完整;
(3)求扇形
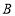 的圆心角度数;
的圆心角度数;(4)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )

A.
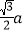 B.
B.  C.
C.  D.
D. 
相关试题

