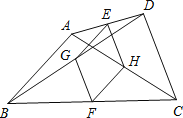
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.

(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)利用三角形的中位线定理可以证得四边形EGFH的四边相等,即可证得;
(2)根据平行线的性质可以证得∠GFH=90°,得到菱形EGFH是正方形,利用三角形的中位线定理求得GE的长,则正方形的面积可以求得.
(1)证明:∵四边形ABCD中,E、F、G、H分别是AD、BC、BD、AC的中点,
∴FG=![]() CD,HE=
CD,HE=![]() CD,FH=
CD,FH=![]() AB,GE=
AB,GE=![]() AB.
AB.
∵AB=CD,
∴FG=FH=HE=EG.
∴四边形EGFH是菱形.
(2)解:∵四边形ABCD中,G、F、H分别是BD、BC、AC的中点,
∴GF∥DC,HF∥AB.
∴∠GFB=∠DCB,∠HFC=∠ABC.
∴∠HFC+∠GFB=∠ABC+∠DCB=90°.
∴∠GFH=90°.
∴菱形EGFH是正方形.
∵AB=1,
∴EG=![]() AB=
AB=![]() .
.
∴正方形EGFH的面积=(![]() )2=
)2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的绝对值等于它的相反数,这个数不会是( )
A. 负整数 B. 负分数 C. 0 D. 正整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为( )
A.30° B.60° C.70° D.150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )

A.
 B.
B. C.
C. D.
D.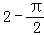
-
科目: 来源: 题型:
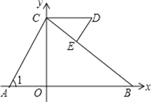
查看答案和解析>>【题目】如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+2b+4的图象经过点(-1,-3),k满足|k-3|=4,且y随x的增大而减小,求此一次函数的表达式.
相关试题

