【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
连接BD,可证△ABE≌△DBF,可得BE=BF,可得△BEF为等边三角形,可得,△BEF的周长为3BE,所以当BE垂直AD时,可求△BEF的周长最小值.
解:连接BD
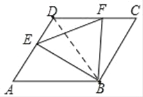
∵ABCD是菱形,∠DAB=60°
∴AB=AD=CD=BC=a,∠C=∠A=60°,∠ADC=∠ABC=120°
∴△ADB,△BDC为等边三角形,
∴∠ADB=∠ABD=60°=∠BDC=∠DBC,AD=BD=a.
∵AE+CF=a,AE+ED=a,CF+DF=a
∴DF=AE,DE=CF,
∵AE=DF,BD=AB,∠A=∠CDB
∴△AEB≌△DFB
∴BE=BF,∠ABE=∠DBF
∵∠ABE+∠DBE=60°
∴∠DBF+∠DBE=60°即∠EBF=60°
∴△BEF为等边三角形.
∴△BEF的周长=3BE
根据垂线段最短,即当BE⊥AD时,BE值最小.
在Rt△AEB中,AB=a,∠A=60°
∴AE=![]() a,BE=
a,BE=![]() a
a
∴△BEF的周长最小值是![]() ,
,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 从点
从点 出发沿
出发沿 方向以
方向以 的速度向点
的速度向点 匀速运动,同时点
匀速运动,同时点 从点
从点 出发沿
出发沿 方向以
方向以 的速度向点
的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 运动的时间是
运动的时间是 .过点
.过点 作
作 于点
于点 连结
连结

(1)求证:
 ;
;(2)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值,如果不能,说明理由;
值,如果不能,说明理由;(3)当
 为何值时,
为何值时, 为直角三角形?请说明理由.
为直角三角形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在“五一”期间,某公司组织318名员工到雷山西江千户苗寨旅游,旅行社承诺每辆车安排有一名随团导游,并为此次旅行安排8名导游,现打算同时租甲、乙两种客车,其中甲种客车每辆载客45人,乙种客车每辆载客30人.
(1)请帮助旅行社设计租车方案.
(2)若甲种客车租金为800元/辆,乙种客车租金为600元/辆,旅行社按哪种方案租车最省钱?此时租金是多少?
(3)旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游随团导游,为保证所租的每辆车安排有一名导游,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案如何安排?
相关试题

