【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.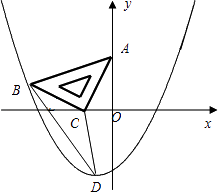
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)(0,2);(﹣3,1)
(2)y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(3)
解:由(2)中抛物线的解析式可知,抛物线的顶点D(﹣ ![]() ,﹣
,﹣ ![]() ),
),
设直线BD的关系式为y=kx+b,将点B、D的坐标代入得:
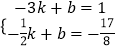 ,
,
解得 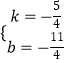 .
.
∴BD的关系式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
设直线BD和x 轴交点为E,则点E(﹣ ![]() ,0),CE=
,0),CE= ![]() .
.
∴S△DBC= ![]() ×
× ![]() ×(1+
×(1+ ![]() )=
)= ![]()
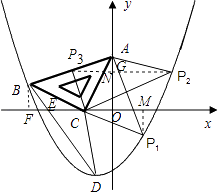
(4)
解:假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCF,∠P1MC=∠BFC=90°,
∴△MP1C≌△FBC.
∴CM=CF=2,P1M=BF=1,
∴P1(1,﹣1);
②若以点A为直角顶点;
i)则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,
∴NP2=OA=2,AN=OC=1,
∴P2(2,1),
ii)若以点P为直角顶点.
过P3作P3G⊥y轴于G,
同理,△AGP3≌△CAO,
∴GP3=OA=2,AG=OC=1,
∴P3为(﹣2,3).
经检验,点P1(1,﹣1)与点P2(2,1)都在抛物线y= ![]() x2+
x2+ ![]() x﹣2上,点P3(﹣2,3)不在抛物线上.
x﹣2上,点P3(﹣2,3)不在抛物线上.
故点P的坐标为P1(1,﹣1)与P2(2,1).
【解析】解:(1)∵C(﹣1,0),AC= ![]() ,
,
∴OA= ![]() =2,
=2,
∴A(0,2);
过点B作BF⊥x轴,垂足为F,
∵∠ACO+∠CAO=90°,∠ACO+∠BCF=90°,∠BCF+∠FBC=90°,
在△AOC与△CFB中,
∵ 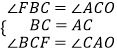 ,
,
∴△AOC≌△CFB,
∴CF=OA=2,BF=OC=1,
∴OF=3,
∴B的坐标为(﹣3,1),
故答案为:(0,2),(﹣3,1);
·(2)∵把B(﹣3,1)代入y=ax2+ax﹣2得:
1=9a﹣3a﹣2,
解得a= ![]() ,
,
∴抛物线解析式为:y= ![]() x2+
x2+ ![]() x﹣2.
x﹣2.
故答案为:y= ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
(1)先根据勾股定理求出OA的长,即可得出点A的坐标,再求出OE、BE的长即可求出B的坐标;(2)把点B的坐标代入抛物线的解析式,求出a的值,即可求出抛物线的解析式;(3)先求出点D的坐标,再用待定系数法求出直线BD的解析式,然后求出CF的长,再根据S△DBC=S△CEB+S△CED进行计算即可;(4)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:
①若以点C为直角顶点;则延长BC至点P1 , 使得P1C=BC,得到等腰直角三角形△ACP1 , 过点P1作P1M⊥x轴,由全等三角形的判定定理可得△MP1C≌△FBC,再由全等三角形的对应边相等可得出点P1点的坐标;
②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2 , 过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,由全等三角形的性质可得出点P2的坐标;点P1、P2的坐标代入抛物线的解析式进行检验即可.
③以点P为直角顶点,求出点P的坐标,再判断点P不在抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.内错角相等,两直线平行).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
上述过程中判定依据错误的是( )
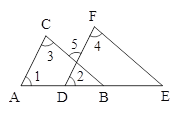
A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧
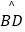 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC=  ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 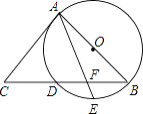
-
科目: 来源: 题型:
查看答案和解析>>【题目】将含30°角的三角板ABC如图放置,使其三个顶点分别落在三条平行直线上,其中∠ACB=90°,当∠1=60°时,图中等于30°的角的个数是()

A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数
1
2
3
4
5
6
出现次数
8
10
7
9
16
10
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
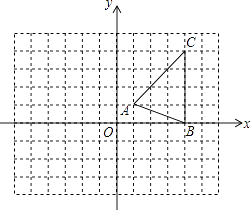
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3÷a2=a3?a﹣2
B.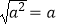
C.2a2+a2=3a4
D.(a﹣b)2=a2﹣b2
相关试题

