【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
参考答案:
【答案】(1)![]() ;(2)丙的说法不正确,理由详见解析;(3)
;(2)丙的说法不正确,理由详见解析;(3)![]() .
.
【解析】
(1)用出现6的次数除总次数即可得解;
(2)丙的说法不正确,理由:(1)因为实验次数较多时,向上点数为![]() 的频率接近于概率,但不说明概率就等一定等于频率;(2)从概率角度来说,向上点数为
的频率接近于概率,但不说明概率就等一定等于频率;(2)从概率角度来说,向上点数为![]() 的概率是
的概率是![]() 的意义是指平均每
的意义是指平均每![]() 次出现
次出现![]() 次;
次;
(3)根据列出表格,由表格得到所有等结果与点数和为3的倍数的情况,然后根据概率公式求解即可.
解:(1)出现向上点数为![]() 的频率:
的频率:![]() ;
;
(2)丙的说法不正确,
理由:(1)因为实验次数较多时,向上点数为![]() 的频率接近于概率,但不说明概率就等一定等于频率;(2)从概率角度来说,向上点数为
的频率接近于概率,但不说明概率就等一定等于频率;(2)从概率角度来说,向上点数为![]() 的概率是
的概率是![]() 的意义是指平均每
的意义是指平均每![]() 次出现
次出现![]() 次;
次;
(3)用表格列出所有等可能性结果:
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
共有![]() 种等可能性结果,其中点数之和为
种等可能性结果,其中点数之和为![]() 的倍数可能性结果有
的倍数可能性结果有![]() 个,
个,
∴![]() (点数之和为
(点数之和为![]() 的倍数)
的倍数)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧
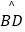 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC=  ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 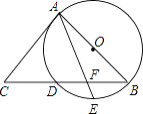
-
科目: 来源: 题型:
查看答案和解析>>【题目】将含30°角的三角板ABC如图放置,使其三个顶点分别落在三条平行直线上,其中∠ACB=90°,当∠1=60°时,图中等于30°的角的个数是()

A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将一块腰长为
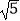 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.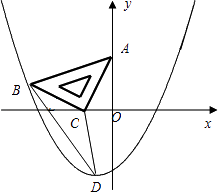
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
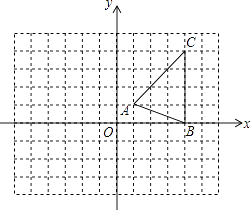
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3÷a2=a3?a﹣2
B.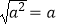
C.2a2+a2=3a4
D.(a﹣b)2=a2﹣b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,BC=4cm,AC=3cm,把△ABC绕点A顺时针旋转90°后,得到△A1B1C1(如图所示),则线段AB所扫过的面积为( )

A.5
B. πcm2
πcm2
C. πcm2
πcm2
D.5πcm2
相关试题

