搜索
【题目】在如图，已知∠1=∠2，∠3=∠4，求证：AC∥DF，BC∥EF.证明过程如下：
∵∠1=∠2（已知），
∴AC∥DF（A．同位角相等，两直线平行），
∴∠3=∠5（B．内错角相等，两直线平行）．
又∵∠3=∠4（已知）
∴∠5=∠4（C．等量代换），
∴BC∥EF（D．内错角相等，两直线平行）．
上述过程中判定依据错误的是（ ）
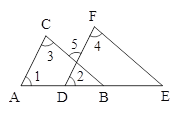
A. A B. B C. C D. D
参考答案：
【答案】B
【解析】
根据平行线的判定与性质逐项分析即可.
∵∠1=∠2（已知），
∴AC∥DF（A．同位角相等，两直线平行），
∴∠3=∠5（B．两直线平行，内错角相等）．
又∵∠3=∠4（已知）
∴∠5=∠4（C．等量代换），
∴BC∥EF（D．内错角相等，两直线平行）．
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，平行四边形ABOC的对角线交于点M，双曲线y=
（x＜0）经过点B、M．若平行四边形ABOC的面积为12，则k= ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】通过学习，同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷．相信通过对下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．
例：用简便方法计算：
．解：
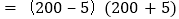①
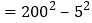②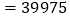
.(1)例题求解过程中，第②步变形是利用___________（填乘法公式的名称）．
(2)用简便方法计算：
． -
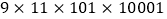科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC=10，BC=12，点D在边BC上，且BD=4，以点D为顶点作∠EDF=∠B，分别交边AB于点E，交AC或延长线于点F．
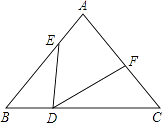
（1）当AE=4时，求AF的长；
（2）当以边AC为直径的⊙O与线段DE相切时，求BE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AC是切⊙O于A的切线，BC交⊙O于点D，E是劣弧
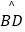的中点，连接AE交BC于点F，若cosC= 
，AC=6，则BF的长为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】将含30°角的三角板ABC如图放置，使其三个顶点分别落在三条平行直线上，其中∠ACB=90°，当∠1=60°时，图中等于30°的角的个数是（）
A. 6个 B. 5个 C. 4个 D. 3个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，将一块腰长为
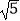的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（﹣1，0），点B在抛物线y=ax2+ax﹣2上．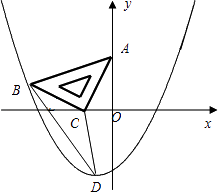
（1）点A的坐标为 ， 点B的坐标为；
（2）抛物线的解析式为；
（3）设（2）中抛物线的顶点为D，求△DBC的面积；
（4）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
相关试题
