【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
参考答案:
【答案】B
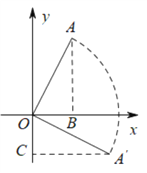
【解析】如图,过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,
∴∠ABO=∠A′CO=90°,
∵点A′是由点A绕点O顺时针旋转90°得到的,
∴∠AOA′=90°,AO=A′O,
∴∠A′OC+∠A′OB=90°,∠A′OB+∠AOB=90°,
∴∠A′OC=∠AOB,
∴△A′OC≌△AOB,
∴OC=OB,A′C=AB,
∵点A的坐标为(1,3),
∴OC=OB=1,A′C=AB=3,
∵点A′在第四象限,
∴点A′的坐标为(3,-1).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
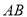 ⊥
⊥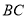 ,
,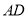 ∥
∥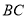 ,
,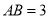 ,
,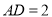 .点
.点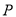 在线段
在线段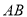 上,联结
上,联结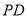 ,过点
,过点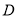 作
作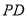 的垂线,与
的垂线,与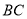 相交于点
相交于点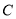 .设线段
.设线段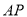 的长为
的长为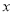 .
.(1)当
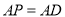 时,求线段
时,求线段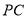 的长;
的长;(2)设△
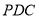 的面积为
的面积为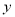 ,求
,求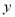 关于
关于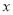 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;(3)当△
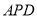 ∽△
∽△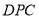 时,求线段
时,求线段 的长.
的长.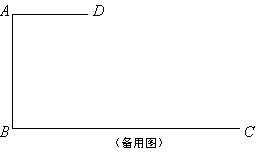
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从A地出发去25km远的B地,甲骑车,乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好为3h.
(1)若设乙的速度为x km/h,则甲的速度为 km/h,甲遇见乙时,乙走的路程可以表示为 km,甲走的路程可以表示为 km.
(2)两人的速度分别是多少?(请用方程来解决问题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
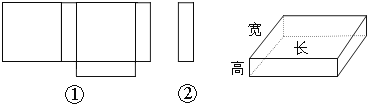
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
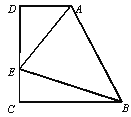
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理绘制成下面的统计图(图1,图2).

小明发现每月每户的用水量在5m3-35m3之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变,根据小明绘制的图表和发现的信息,完成下列问题:
(Ⅰ)n= ,小明调查了 户居民,并补全图2;
(Ⅱ)每月每户用水量的中位数和众数分别落在什么范围?
(Ⅲ)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=
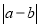 ,线段AB的中点表示的数为
,线段AB的中点表示的数为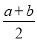 .
.(问题情境)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(综合运用)(1)点B表示的数是__________.
(2)若BC:AC=4:7,求点C到原点的距离.
(3)如图2,在(2)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(4)如图3,在(2)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒,1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT-MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.

相关试题

