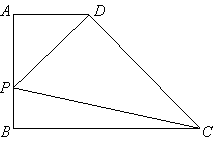
【题目】已知:如图,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 相交于点
相交于点![]() .设线段
.设线段![]() 的长为
的长为![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)设△![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△![]() ∽△
∽△![]() 时,求线段
时,求线段![]() 的长.
的长.
参考答案:
【答案】(1)![]() (2)
(2)![]() ,0 < x ≤ 3(3)4或
,0 < x ≤ 3(3)4或![]()
【解析】(1)过点![]() 作
作![]() ⊥
⊥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() ,
,![]() ,PD⊥CD,AD // BC,
,PD⊥CD,AD // BC,
∴∠![]() =∠
=∠![]() =∠
=∠![]() = 90°,
= 90°,
![]() .
.
∵![]() //
// ![]() ,
,
∴![]() .即得
.即得![]() .
.
又∵![]() ,
,
![]() ,
,
∴![]() .
.
又由![]() ,得 △
,得 △![]() ∽△
∽△![]() .
.
∴![]() .
.
于是,由![]() ,得
,得 ![]() . (2分)
. (2分)
在![]() △
△![]() 和
和![]() △
△![]() 中,
中,
得 ![]() ,
,![]() . (1分)
. (1分)
于是,在![]() △
△![]() 中,得
中,得 ![]() . (1分)
. (1分)
(2)在Rt△![]() 中,由
中,由 ![]() ,
,![]() ,
,
得![]() . (1分)
. (1分)
∵△![]() ∽△
∽△![]() ,
,
∴![]() .
.
∴![]() . (1分)
. (1分)
在![]() △
△![]() 中,
中,![]() .
.
∴所求函数解析式为![]() . (2分)
. (2分)
函数的定义域为 0 < x ≤ 3. (1分)
(3)当△![]() ∽△
∽△![]() 时,即得△img src="http://thumb.zyjl.cn/questionBank/Upload/2019/04/06/13/515cbe93/SYS201904061302267942123906_DA/SYS201904061302267942123906_DA.035.png" width="37" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∽△
时,即得△img src="http://thumb.zyjl.cn/questionBank/Upload/2019/04/06/13/515cbe93/SYS201904061302267942123906_DA/SYS201904061302267942123906_DA.035.png" width="37" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∽△![]() ∽△
∽△![]() . (1分)
. (1分)
根据题意,当△![]() ∽△
∽△![]() 时,有下列两种情况:
时,有下列两种情况:
(ⅰ)当点![]() 与点
与点![]() 不重合时,可知
不重合时,可知 ![]() .
.
由△![]() ∽∽△
∽∽△![]() ,得
,得![]() .即得
.即得![]() .
.
由△![]() ∽△
∽△![]() ,得
,得![]() .
.
∴![]() .即得
.即得![]() .
.
∴![]() .
.
易证得四边形![]() 是矩形,
是矩形,
∴![]() . (2分)
. (2分)
(ⅱ)当点![]() 与点
与点![]() 重合时,可知
重合时,可知 ![]() .
.
在Rt△![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() .
.
由△![]() ∽△
∽△![]() ,得
,得![]() .
.
即得![]() .
.
解得![]() . (2分)
. (2分)
∴△![]() ∽△
∽△![]() 时,线段
时,线段![]() 的长分别为4或
的长分别为4或![]() .
.
(1)过点![]() 作
作![]() ⊥
⊥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,证出△
,证出△![]() ∽△
∽△![]() ,从而得出DE的长,然后根据勾股定理得出PD与DC的长,再根据勾股定理得出PC的长;
,从而得出DE的长,然后根据勾股定理得出PD与DC的长,再根据勾股定理得出PC的长;
(2)先求出PD的长,然后根据△![]() ∽△
∽△![]() ,算出CD的长,再利用三角形面积公式得出它的解析式;
,算出CD的长,再利用三角形面积公式得出它的解析式;
(3)分点P与点B重合不重合两种情况进行讨论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

-
科目: 来源: 题型:
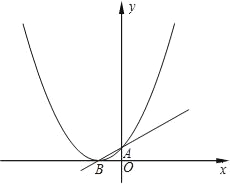
查看答案和解析>>【题目】已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
(1)求这个函数关系式;
(2)如图所示,设二次函数y=ax2+x+1图象的顶点为B,与y轴的交点为A,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;
(3)在(2)中,若圆与x轴另一交点关于直线PB的对称点为M,试探索点M是否在抛物线y=ax2+x+1上?若在抛物线上,求出M点的坐标;若不在,请说明理由.
-
科目: 来源: 题型:
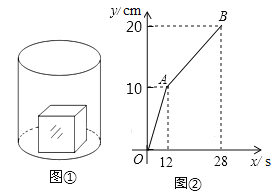
查看答案和解析>>【题目】(2017·吉林)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从A地出发去25km远的B地,甲骑车,乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好为3h.
(1)若设乙的速度为x km/h,则甲的速度为 km/h,甲遇见乙时,乙走的路程可以表示为 km,甲走的路程可以表示为 km.
(2)两人的速度分别是多少?(请用方程来解决问题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
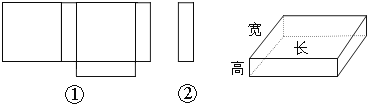
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
相关试题

