【题目】甲、乙两人同时从A地出发去25km远的B地,甲骑车,乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好为3h.
(1)若设乙的速度为x km/h,则甲的速度为 km/h,甲遇见乙时,乙走的路程可以表示为 km,甲走的路程可以表示为 km.
(2)两人的速度分别是多少?(请用方程来解决问题)
参考答案:
【答案】(1)乙走的路程可以表示为3xkm,甲走的路程可以表示为(3-![]() )×3xkm.
)×3xkm.
(2)甲的速度为15千米小时,乙的速度为5千米小时
【解析】
(1)根据题意找到甲的速度是乙的速度的3倍,再利用甲到达B地停留40min后在途中遇见乙,列代数式即可解题,
(2)根据相遇时甲走过的路程+乙走过的路程=50km,即可解题.
解:(1)若设乙的速度为x km/h,
∵甲的速度是乙的速度的3倍,
∴甲的速度为3xkm/h,
∵3小时候相遇,甲到达B地停留40min=![]() h,
h,
∴甲遇见乙时,乙走的路程可以表示为3xkm,甲走的路程可以表示为(3-![]() )×3xkm.
)×3xkm.
(2)由(1)可知,3x+(3-![]() )×3x =25×2,
)×3x =25×2,
解得x=5,
∴甲的速度为15千米小时,乙的速度为5千米小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
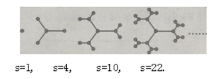
A.162B.176C.190D.214
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=
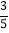
 ,求⊙O半径的长.
,求⊙O半径的长.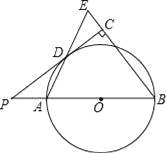
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab+2ab+a. 如:13=1×3+2×1×3+1=16
(1)求3(﹣1)的值;
(2)若(a+1)2=36,求a的值;
(3)若m=2x,n=(
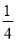 x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若点C在直线AB上,且
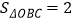 ,求点C的坐标.
,求点C的坐标.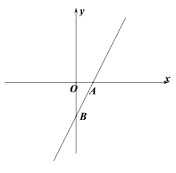
-
科目: 来源: 题型:
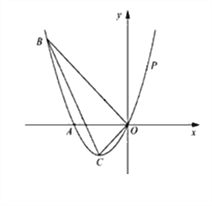
查看答案和解析>>【题目】如图,已知抛物线经过A(-2,0)B(-3,3)及原点O,顶点为C。
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标。
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥ x轴,垂足为M,是否存在点P点使得以P、M、A为顶点的三角形与△BOC相似?若存在,求P点的坐标,若不存在,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4
 ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.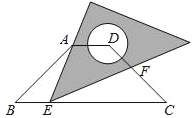
相关试题

