【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=![]() ,线段AB的中点表示的数为
,线段AB的中点表示的数为![]() .
.
(问题情境)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(综合运用)(1)点B表示的数是__________.
(2)若BC:AC=4:7,求点C到原点的距离.
(3)如图2,在(2)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(4)如图3,在(2)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒,1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT-MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.

参考答案:
【答案】(1)-20;(2)100;(3)9个单位长度/秒;(4)PT-MN的值不变,值为30.
【解析】
(1)根据AB=60,点A对应的数是40,得出点B对应的数;(2)根据AB=60,BC:AC=4:7,得出BC=80,利用点A对应的数是40,即可得出点C对应的数;(3)假设点R速度为a单位长度/秒,根据点P、Q之间的距离与点Q、R的距离相等,得出等式方程求出即可;(4)分别表示出PT,MN的值,进而求出PT-MN的值;
解:
(1)∵AB=60,点A对应的数是40,
∴点B对应的数为:40-60=-20;
故答案为-20;
(2)∵BC:AC=4:7,
∴BC:AB=4:3,
∵AB=60,
∴BC=80,
∴AC=140,
∵点A对应的数是40,
∴点C对应的数为40-140=-100;
∴C到原点的距离为100;
故答案为100;
(3)设R的速度为a个单位长度/秒,则P的速度为3a个单位长度/秒,Q的速度为(2a-5)个单位长度/秒;
由题意得:![]() ,
,
解得:![]() ,
,
![]() ,
,
答:Q的速度为9个单位长度/秒.
(4)PT-MN的值不变;
理由如下:设运动时间为t 秒,则P:![]() ,
,
T:![]() ,
,
M:![]() ,
,
O:0,
R:![]() ,
,
N:![]() ,
,
PT![]() ,
,
MN![]() ,
,
PT-MN![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
-
科目: 来源: 题型:
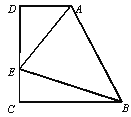
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC (BC>AD),∠D=90°,∠ABE=45°,BC=CD,
若AE=5,CE=2,则BC的长度为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理绘制成下面的统计图(图1,图2).

小明发现每月每户的用水量在5m3-35m3之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变,根据小明绘制的图表和发现的信息,完成下列问题:
(Ⅰ)n= ,小明调查了 户居民,并补全图2;
(Ⅱ)每月每户用水量的中位数和众数分别落在什么范围?
(Ⅲ)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】城南中学九年级共有12个班,每班48名学生,学校对该年级学生数学学科学业水平测试成绩进行了抽样分析,请按要求回答下列问题:
【收集数据】
(1)要从九年级学生中抽取一个48人的样本,你认为以下抽样方法中最合理的是
________.①随机抽取一个班级的48名学生;②在九年级学生中随机抽取48名女学生;
③在九年级12个班中每班各随机抽取4名学生.
【整理数据】
(2)将抽取的48名学生的成绩进行分组,绘制成绩频数分布表和成绩分布扇形统计图如下.
请根据图表中数据填空:
①表中m的值为________;
② B类部分的圆心角度数为________°;
③估计C、D类学生大约一共有_________名.

九年级学生数学成绩频数分布表
成绩(单位:分)
频数
频率
A类(80~100)
24

B类(60~79)
12
C类(40~59)
8
m
D类(0~39)
4
【分析数据】
(3)教育主管部们为了解学校学生成绩情况,将同层次的城南、城北两所中学的抽样数据进行对比分析,得到下表:
学校
平均数(分)
方差
A、B类的频率和
城南中学
71
358
0.75
城北中学
71
588
0.82
请你评价这两所学校学生数学学业水平测试的成绩,提出一个解释来支持你的观点.
-
科目: 来源: 题型:
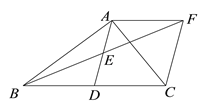
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中处处有数学,下列原理运用错误的是
 .
.A.建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理
B.修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理
C.测量跳远的成绩是运用“垂线段最短”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”原理
相关试题

