【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
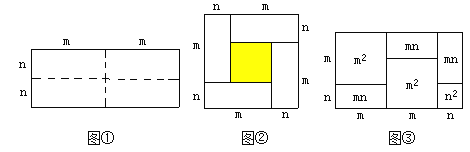
(1)、你认为图②中的阴影部分的正方形的边长等于________;
(2)、请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;
方法②: ;
(3)、请你观察图②,利用图形的面积写出![]() 、
、![]() 、mn这三个代数式之间的等量关系: ;
、mn这三个代数式之间的等量关系: ;
(4)、根据(3)中的结论,若x+y=-8,xy=3.75,则x-y= ;
(5)、有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了(2m+n)(m+n)=2![]() +3mn+
+3mn+![]() .
.
试画出一个几何图形,使它的面积能表示:(2m+n)(m+2n)=2![]() +5mn+2
+5mn+2![]() .
.
参考答案:
【答案】(1)、m-n;(2)、![]() ;
;![]() -4mn;(3)、
-4mn;(3)、![]() =
=![]() -4mn;(4)、±7;(5)、答案见解析
-4mn;(4)、±7;(5)、答案见解析
【解析】
试题分析:(1)、小正方形的边长等于长方形的长减去长方形的宽;(2)、阴影部分的面积等于小正方形边长的平方,也等于大正方形的面积减去4个长方形的面积;(3)、根据面积相等列出等式;(4)、根据所列的等式求出x-y的值;(5)、画出的矩形的两边长分别为(2m+n)和(m+2n).
试题解析:(1)、m-n;
(2)、![]() ;
;![]() -4mn;
-4mn;
(3)(3)、![]() =
=![]() -4mn;
-4mn;
(4)、x-y=±![]() =±
=±![]() =±7.
=±7.
(5)、
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设图中每个小正方形的边长为1,
(1)请画出△ABC关于y轴对称图形△A’B’C’,其中ABC的对称点分别为A’B’C’)
(2)直接写出A’B’C’的坐标:A’B’C’
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
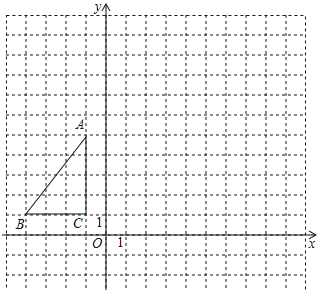
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)、
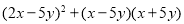 ,其中
,其中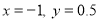
(2)、
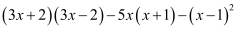 ,其中
,其中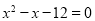
(3)、已知
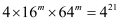 ,求
,求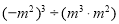 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(x1,y1)和B(x2,y2)都在直线y=3x+2上,且x1>x2,则y1与y2的关系是( )
A. y1≤y2 B. y1≥y2 C. y1<y2 D. y1>y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示整数的点称为整数点,某数轴的单位长度是1㎝,若在这个数轴上随意画出一条长2009㎝的线段AB,被线段AB盖住的整数有( )
A.2006个或2007个
B.2007个或2008个
C.2008个或2009个
D.2009个或2010个 -
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
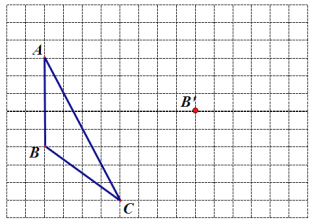
(1)请画出平移后的△A′B′C′.
(2)若连接AA′,CC′,则这两条线段之间的关系是________.
(3)利用网格画出△ABC 中AC边上的中线BD
(4)利用网格画出△ABC 中AB边上的高CE.
(5)△A′B′C′的面积为 。
相关试题

