搜索
【题目】已知二次函数的图像经过点（0，3）、（3，0）和（1，4）．
（1）求该二次函数的表达式；
（2）若该二次函数图像的顶点为P，与x轴分别交于点A、B，求△ABP的面积．
参考答案：
【答案】（1）y=－x2+2x+3；（2）8．
【解析】分析：（1）设二次函数解析式y=ax2+ax+c,把三点坐标代入求出a,b,c的值，即可确定出二次函数解析式；（2）令y=0,求得点A,B的坐标，根据三角形的面积公式来求△ABP的面积.
本题解析：（1）设二次函数解析式y=ax2+ax+c，∵将点（0,3）、（3,0）和（1,4）
代入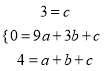得
，解得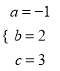
，∴y=－x2+2x+3；
（2）y=－x2+2x+3= -(x-1)+4, ∴p为二次函数顶点，∴p(1,4),令y=0，即－x2+2x+3=0，（x-3）（x+1）=0， 
，∴A,B两点坐标为（-1,0），（3,0），∴AB=4，∴
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，点B在x轴上，且
．
求点B的坐标；
求
的面积；
在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图点A（a，0）在x轴负半轴，点B（b，0）在x轴正半轴，点C（0，c）在y轴正半轴，且
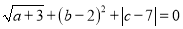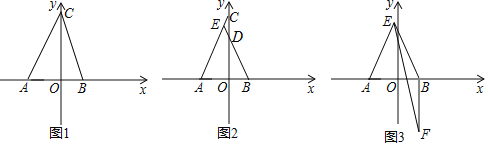
．（1）如图1，求S△ABC；
（2）如图2，若点D（0，5），BD的延长线交AC于E，求∠AEB；
（3）如图3，在（2）的条件下，将线段BA绕点B逆时针旋转90°至线段BF，连接EF，试探究EA，EB，EF之间有怎样的数量关系，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在菱形ABCD中，M是BC边上的点（不与B，C两点重合），AB=AM，点B关于直线AM对称的点是N，连接DN，设∠ABC，∠CDN的度数分别为
，
，则关于的函数解析式是_______________________________． -
科目： 来源： 题型：
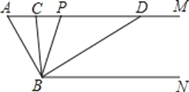
查看答案和解析>>【题目】如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
（1）求∠CBD的度数；
（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
（3）当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知⊙O的直径为10，点A、B、C在⊙O上，∠CAB的平分线交⊙O于点D．
（1）图①，当BC为⊙O的直径时，求BD的长；
（2）图②，当BD＝5时，求∠CDB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y＝x2＋（k－1）x－2k－3．
（1）求证：该二次函数图像与x轴总有两个公共点；
（2）若点A（－1，y1）、B（1，y2）在该二次函数的图像上，且y1＞y2，求k的取值范围．
相关试题
