【题目】如图,已知⊙O的直径为10,点A、B、C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)图①,当BC为⊙O的直径时,求BD的长;
(2)图②,当BD=5时,求∠CDB的度数.

参考答案:
【答案】(1)![]() ;(2)120°.
;(2)120°.
【解析】分析;(1)连接CD,只要证明△ABD是等腰三角形是解题关键;(2)首先证明△OBD是等边三角形,推出∠BOD=60°,由![]() ,推出∠ACD=∠BAD=30°,推出∠BAC=60°,再利用圆内接四边形的性质即可解决问题.
,推出∠ACD=∠BAD=30°,推出∠BAC=60°,再利用圆内接四边形的性质即可解决问题.
本题解析:
解:(1)连接CD
∵∠CAB的平分线交⊙O于点D,∴∠CAD=∠DAB;
∴![]() =
=![]()
∴CD=DB
∵BC为⊙O的直径
∴∠CDB=90°
在Rt△CDB中,CD2+BD2=BC2
∴BD =5![]() .
.
(2)连接OB、OD
∵⊙O直径为10,∴ OB=OD=5
∵BD=5
∴ OB=OD= BD
∴ △BOD为等边三角形
∴ ∠BOD=60°
∵![]() =
=![]()
∴∠ACD=∠BAD=30°
∴∠BAC=60°
∵四边形ABDC是⊙O的内接四边形
∴∠CDB=180°﹣∠BAC =120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,M是BC边上的点(不与B,C两点重合),AB=AM,点B关于直线AM对称的点是N,连接DN,设∠ABC,∠CDN的度数分别为
 ,
, ,则
,则 关于
关于 的函数解析式是_______________________________.
的函数解析式是_______________________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图像经过点(0,3)、(3,0)和(1,4).
(1)求该二次函数的表达式;
(2)若该二次函数图像的顶点为P,与x轴分别交于点A、B,求△ABP的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
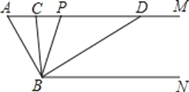
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+(k-1)x-2k-3.
(1)求证:该二次函数图像与x轴总有两个公共点;
(2)若点A(-1,y1)、B(1,y2)在该二次函数的图像上,且y1>y2,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD为△ABC的中线,O为AB上一点,以O为圆心,AO为半径的⊙O与AB交于点F,与BC交于点E.连接AE,AE平分∠BAD.
(1)求证:BC与⊙O相切于点E;
(2)若AB=10,BC=16,求⊙O的半径;
(3)若AD与⊙O的交点为△ABC的重心,则
 的值为 .
的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店经营某种水果,顾客的批发量x(kg)与批发单价y(元/kg)之间的关系如图所示.图中线段AB表示:批发量x每增加1 kg,批发单价y降低0.1元/kg.
(1)求m的值;
(2)已知该水果进价为6元/kg,设该水果店获利w元.
①求w与x的函数表达式;
②当0<x≤m时,求w的最大值.

相关试题

