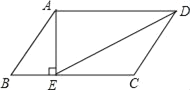
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

参考答案:
【答案】①②③
【解析】
利用平行四边形的性质结合勾股定理以及三角形面积求法分别分析得出答案.
解:①∵在ABCD中,AE⊥BC,垂足为E,AE=4,BC=8,
∴AD=8,∠EAD=90°,
∴DE=![]() =
=![]() ,故此选项正确;
,故此选项正确;
②∵S△AED=![]() AEAD
AEAD
S四边形ABCD=AE×AD,
∴S△AED=![]() S四边形ABCD,故此选项正确;
S四边形ABCD,故此选项正确;
③∵AD∥BC,
∴∠ADE=∠DEC,
∵AB=5,AE=4,∠AEB=90°,
∴BE=3,
∵BC=8,
∴EC=CD=5,
∴∠CED=∠CDE,
∴∠ADE=∠CDE,
∴DE平分∠ADC,故此选项正确;
④当∠AED=∠ADC时,由③可得∠AED=∠EDC,
故AE∥DC,与已知AB∥DC矛盾,故此选项错误.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点在x轴上,顶点B在y轴上,顶点C在函数
 (x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点
(x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点 落在此函数的图象上,则平移的距离为 .
落在此函数的图象上,则平移的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在透明纸面上有一数轴(如图1),折叠透明纸面.
(1)若表示
 的点与表示
的点与表示 的点重合,则表示
的点重合,则表示 的点与表示_________的点重合;
的点与表示_________的点重合;(2)若表示
 的点与表示
的点与表示 的点重合,回答以下问题:
的点重合,回答以下问题:①表示
 的点与表示__的点重合;
的点与表示__的点重合;②如图2,若数轴上
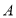 、
、 两点之间的距离为
两点之间的距离为 (点
(点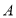 在点
在点 的左侧),且
的左侧),且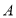 、
、 两点经折叠后重合,则
两点经折叠后重合,则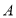 、
、 两点表示的数分别是_________、_________.
两点表示的数分别是_________、_________.(3)如图3,若
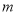 和
和 表示的点
表示的点 和点
和点 经折叠后重合
经折叠后重合 ,折痕与数轴的交点为折痕点.已知线段
,折痕与数轴的交点为折痕点.已知线段 上两点
上两点 、
、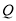 (点
(点 在点
在点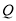 的左侧,
的左侧,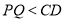 ),
), .当线段
.当线段 的端点与折痕点重合时,求
的端点与折痕点重合时,求 、
、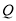 两点表示的数分别是多少?(用含
两点表示的数分别是多少?(用含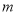 ,
, ,
, 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=
 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两站相距480千米,一辆快车从甲站出发,每小时行驶120千米,一辆慢车从乙站出发,每小时行驶80千米.
(1)两车同时开出,相向而行,多少小时后两车相遇?
(2)两车同时开出,相向而行,多少小时后两车相距100千米?
-
科目: 来源: 题型:
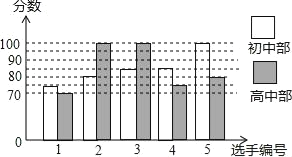
查看答案和解析>>【题目】某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
平均数(分)
中位数(分)
众数(分)
初中代表队
85
85
高中代表队
80
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一
星期二
星期三
星期四
星期五
+11
+10
﹣17
+18
﹣12
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
相关试题

