【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.

(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
参考答案:
【答案】(1)反比例函数解析式为:y=![]() ;(2)P(5,0);(3)Q点坐标为:(
;(2)P(5,0);(3)Q点坐标为:(![]() ,0).
,0).
【解析】
试题(1)利用已知点B坐标代入一次函数解析式得出答案,再利用△OBM的面积得出M点纵坐标,再利用相似三角形的判定与性质得出M点坐标即可得出反比例函数解析式;
(2)过点M作PM⊥AM,垂足为M,得出△AOB∽△PMB,进而得出BP的长即可得出答案;
(3)利用△QBM∽△OAM,得出![]() =
=![]() ,进而得出OQ的长,即可得出答案.
,进而得出OQ的长,即可得出答案.
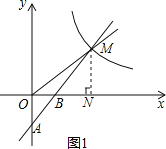
解:(1)如图1,过点M作MN⊥x轴于点N,
∵一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,
∴0=k1﹣1,AO=BO=1,
解得:k1=1,
故一次函数解析式为:y=x﹣1,
∵△OBM的面积为1,BO=1,
∴M点纵坐标为:2,
∵∠OAB=∠MNB,∠OBA=∠NBM,
∴△AOB∽△MNB,
∴![]() =
=![]() =
=![]() ,
,
则BN=2,
故M(3,2),
则xy=k2=6,
故反比例函数解析式为:y=![]() ;
;
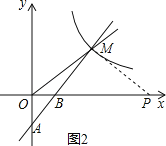
(2)如图2,过点M作PM⊥AM,垂足为M,
∵∠AOB=∠PMB,∠OBA=∠MBP,
∴△AOB∽△PMB,
∴![]() =
=![]() ,
,
由(1)得:AB=![]() =
=![]() ,BM=
,BM=![]() =2
=2![]() ,
,
故![]() =
=![]() ,
,
解得:BP=4,
故P(5,0);
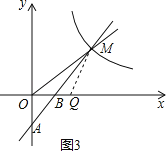
(3)如图3,∵△QBM∽△OAM,
∴![]() =
=![]() ,
,
由(2)可得AM=3![]() ,
,
故![]() =
=![]() ,
,
解得:QB=![]() ,
,
则OQ=![]() ,
,
故Q点坐标为:(![]() ,0).
,0).
-
科目: 来源: 题型:
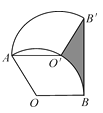
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点在x轴上,顶点B在y轴上,顶点C在函数
 (x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点
(x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点 落在此函数的图象上,则平移的距离为 .
落在此函数的图象上,则平移的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在透明纸面上有一数轴(如图1),折叠透明纸面.
(1)若表示
 的点与表示
的点与表示 的点重合,则表示
的点重合,则表示 的点与表示_________的点重合;
的点与表示_________的点重合;(2)若表示
 的点与表示
的点与表示 的点重合,回答以下问题:
的点重合,回答以下问题:①表示
 的点与表示__的点重合;
的点与表示__的点重合;②如图2,若数轴上
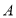 、
、 两点之间的距离为
两点之间的距离为 (点
(点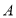 在点
在点 的左侧),且
的左侧),且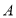 、
、 两点经折叠后重合,则
两点经折叠后重合,则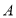 、
、 两点表示的数分别是_________、_________.
两点表示的数分别是_________、_________.(3)如图3,若
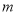 和
和 表示的点
表示的点 和点
和点 经折叠后重合
经折叠后重合 ,折痕与数轴的交点为折痕点.已知线段
,折痕与数轴的交点为折痕点.已知线段 上两点
上两点 、
、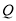 (点
(点 在点
在点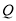 的左侧,
的左侧,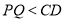 ),
), .当线段
.当线段 的端点与折痕点重合时,求
的端点与折痕点重合时,求 、
、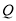 两点表示的数分别是多少?(用含
两点表示的数分别是多少?(用含 ,
, ,
, 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4
 ;
;②S△AED=
 S四边形ABCD;
S四边形ABCD;③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两站相距480千米,一辆快车从甲站出发,每小时行驶120千米,一辆慢车从乙站出发,每小时行驶80千米.
(1)两车同时开出,相向而行,多少小时后两车相遇?
(2)两车同时开出,相向而行,多少小时后两车相距100千米?
-
科目: 来源: 题型:
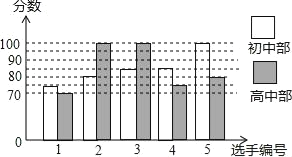
查看答案和解析>>【题目】某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
平均数(分)
中位数(分)
众数(分)
初中代表队
85
85
高中代表队
80
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.
相关试题

