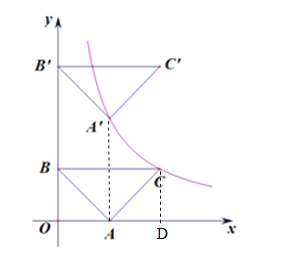
【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点在x轴上,顶点B在y轴上,顶点C在函数![]() (x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点
(x>0)的图象上,且BC∥x轴.将△ABC沿y轴正方向平移,使点A的对应点![]() 落在此函数的图象上,则平移的距离为 .
落在此函数的图象上,则平移的距离为 .

参考答案:
【答案】4
【解析】解:连接AA′,过C作CD⊥x轴于D.∵△ABC是等腰直角三角形,∴AB=AC,∠CBA=∠CBA=45°.∵BC∥x轴,∴∠BAO=∠CAD=45°.∵∠BOA=∠CDA=90°,∴△BOA≌△CDA,∴OB=OA=AD=CD,设OA=a,则OD=2a,CD=a,∴C(2a,a).∵C在![]() 上,∴
上,∴![]() ,解得:a=±2(负数舍去),∴a=2.
,解得:a=±2(负数舍去),∴a=2.
设AA′=x,则A′(2,x),∴![]() =4.故答案为:4.
=4.故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设
 ,
, ,
, ,请探索
,请探索 ,
, ,
, 满足的等量关系。
满足的等量关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=
 的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣
的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣ <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
-
科目: 来源: 题型:
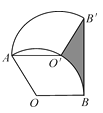
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在透明纸面上有一数轴(如图1),折叠透明纸面.
(1)若表示
 的点与表示
的点与表示 的点重合,则表示
的点重合,则表示 的点与表示_________的点重合;
的点与表示_________的点重合;(2)若表示
 的点与表示
的点与表示 的点重合,回答以下问题:
的点重合,回答以下问题:①表示
 的点与表示__的点重合;
的点与表示__的点重合;②如图2,若数轴上
 、
、 两点之间的距离为
两点之间的距离为 (点
(点 在点
在点 的左侧),且
的左侧),且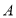 、
、 两点经折叠后重合,则
两点经折叠后重合,则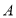 、
、 两点表示的数分别是_________、_________.
两点表示的数分别是_________、_________.(3)如图3,若
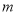 和
和 表示的点
表示的点 和点
和点 经折叠后重合
经折叠后重合 ,折痕与数轴的交点为折痕点.已知线段
,折痕与数轴的交点为折痕点.已知线段 上两点
上两点 、
、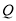 (点
(点 在点
在点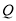 的左侧,
的左侧,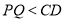 ),
), .当线段
.当线段 的端点与折痕点重合时,求
的端点与折痕点重合时,求 、
、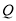 两点表示的数分别是多少?(用含
两点表示的数分别是多少?(用含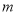 ,
, ,
, 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=
 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4
 ;
;②S△AED=
 S四边形ABCD;
S四边形ABCD;③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

相关试题

