【题目】用一条长为18的绳子围成一个等腰三角形.
(1)若等腰三角形有一条边长为4,它的其它两边是多少?
(2)若等腰三角形的三边长都为整数,请直接写出所有能围成的等腰三角形的腰长.
参考答案:
【答案】(1)其他两边分别为4和7;(2)y=2时,x=8,y=4时,x=7,y=8时,x=5.
【解析】
(1)根据等腰三角形的性质即可求出答案.
(2)设等腰三角形的三边长为x、x、y,根据题意可知y<9,y是2的倍数,从而可求出答案.
解:(1)当等腰三角形的腰长为4,
∴底边长为18﹣4×2=10,
∵4+4<10,
∴4、4、10不能组成三角形,
当等腰三角形的底边长为4,
∴腰长为(18﹣4)÷2=7,
∵4+7>7,
∴4、7、7能组成三角形,
综上所述,其他两边分别为4和7.
(2)设等腰三角形的三边长为x、x、y,
由题意可知:2x+y=18,
且2x>y,
∴y<9,
∵x=![]() =9﹣
=9﹣![]() ,x与y都是整数,
,x与y都是整数,
∴y是2的倍数,
∴y=2时,x=8,
y=4时,x=7,
y=8,x=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2 .
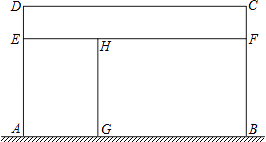
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是
是 的高,直线
的高,直线 相交所成的角中有一个角为50°,则
相交所成的角中有一个角为50°,则 的度数为________.
的度数为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.
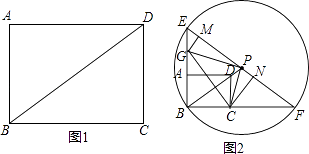
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数中,y的值随着x值的增大而减小的是( )
A.y=2x
B.y=x+1
C.y= (x>0)
(x>0)
D.y=x2(x>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A、B两种商品很快售完,该商场决定再一次购进A、B两种商品共35件,如果将这35件商品全部售完后所得利润高于4000元,那么该商场至少需购进多少件A种商品?
相关试题

