【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.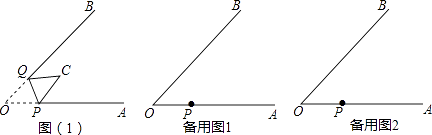
(1)当PC∥QB时,OQ=;
(2)当PC⊥QB时,求OQ的长.
(3)当折叠后重叠部分为等腰三角形时,求OQ的长.
参考答案:
【答案】
(1)2cm
(2)解:当PC⊥QB时,分两种情况:
(i)如图1所示:
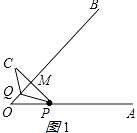
设OQ=xcm,
∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM= ![]() OP=
OP= ![]() ,
,
∴QM= ![]() ﹣x,
﹣x,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,
∴△CQM是等腰直角三角形,
∴QC= ![]() QM
QM
∴x= ![]() (
( ![]() ﹣x),
﹣x),
解得:x=2 ![]() ﹣2,
﹣2,
即OQ=2 ![]() ﹣2;
﹣2;
(ii)如图2所示:
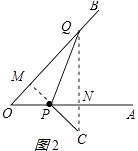
同(i)得:OQ=2 ![]() +2;
+2;
综上所述:当PC⊥QB时,OQ的长为2 ![]() ﹣2,或2
﹣2,或2 ![]() +2
+2
(3)
解:当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ= ![]() 或2
或2 ![]() ;
;
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:
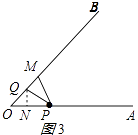
PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,
由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ= ![]() a,PN=
a,PN= ![]() QN=
QN= ![]() a,
a,
∵ON+PN=OP,
∴a+ ![]() a=2,
a=2,
解得:a= ![]() ﹣1,
﹣1,
∴OQ= ![]() (
( ![]() ﹣1)=
﹣1)= ![]() ﹣
﹣ ![]() ;
;
(ii)如图4所示:
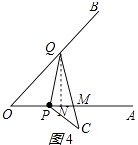
PQ=MQ,作QN⊥OA于N,
同①得:OQ= ![]() +
+ ![]() ;
;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或(2 ![]() ﹣2,)cm或(2
﹣2,)cm或(2 ![]() +2)cm或(
+2)cm或( ![]() ﹣
﹣ ![]() )cm或(
)cm或( ![]() +
+ ![]() )cm.
)cm.
【解析】解:(1)当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
所以答案是:2cm;
-
科目: 来源: 题型:
查看答案和解析>>【题目】要在一块长52m,宽48m的矩形绿地上,修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案.
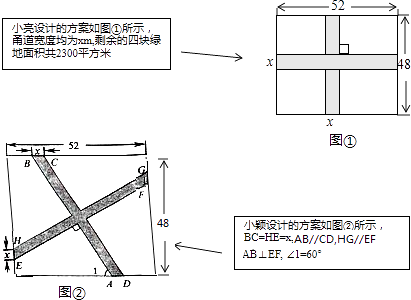
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同) -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在y轴的正半轴上,点A在x轴的正半轴上,点C的坐标为(0,8),将△ABC沿直线AB折叠,点C落在x轴的负半轴D(﹣4,0)处.
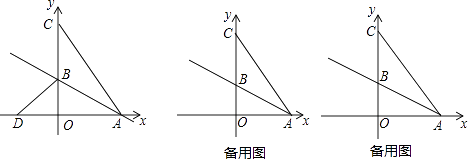
(1)求直线AB的解析式;
(2)点P从点A出发以每秒4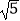 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);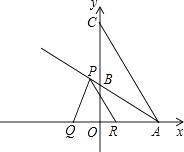
(3)在(2)的条件下,点N是射线AB上一点,以点N为圆心,同时经过R、Q两点作⊙N,⊙N交y轴于点E,F.是否存在t,使得EF=RQ?若存在,求出t的值,并求出圆心N的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格线的交点叫格点,格点
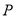 是
是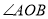 的边
的边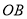 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).
(1)过点
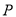 画
画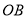 的垂线,交
的垂线,交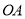 于点
于点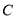 ;
;(2)线段 的长度是点O到PC的距离;
(3)
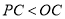 的理由是 ;
的理由是 ; (4)过点C画
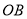 的平行线;
的平行线; -
科目: 来源: 题型:
查看答案和解析>>【题目】a
 b是新规定的一种运算法则:a
b是新规定的一种运算法则:a b=a2+ab,例如3
b=a2+ab,例如3 (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.(1)求(﹣3)
 5的值;
5的值;(2)若(﹣2)
 x=6,求x的值;
x=6,求x的值;(3)若3
 (2
(2 x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,AC∥DF,AC=DF,添加下列条件,不能判断 △ABC≌△DEF的是( )
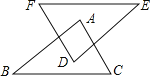
A. EF=BC B. AB=DE C. EF∥BC D.
 B=
B= E
E
相关试题

