【题目】某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由

参考答案:
【答案】(1)、5元;(2)、20000元;2.5元;(3)、y1=5x;y2=2.5x+20000;(4)、当x=8000时,两种方案同样省钱;当x<8000时,选择方案一;当x>8000时,选择方案二.
【解析】试题分析:(1)、根据图一得出答案;(2)、根据图二得出租赁机器的费用和盒子的单价;(3)、利用待定系数法分别求出两个函数的解析式;(4)、首先求出两个相等时x的值,然后得出答案.
试题解析:(1)、500÷100=5, ∴方案一的盒子单价为5元;
(2)、根据函数的图象可以知道租赁机器的费用为20000元,
盒子的单价为(30000﹣20000)÷4000=2.5, 故盒子的单价为2.5元;
(3)、设图象一的函数解析式为:y1=k1x, 由图象知函数经过点(100,500), ∴500=100k1,
解得k1=5, ∴函数的解析式为y1=5x;
设图象二的函数关系式为y2=k2x+b
由图象知道函数的图象经过点(0,20000)和(4000,30000)∴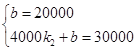 ,
,
解得: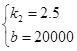 , ∴函数的解析式为y2=2.5x+20000;
, ∴函数的解析式为y2=2.5x+20000;
(4)、令5x=2.5x+20000, 解得x=8000,
∴当x=8000时,两种方案同样省钱;当x<8000时,选择方案一;当x>8000时,选择方案二.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
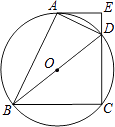
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
-
科目: 来源: 题型:
查看答案和解析>>【题目】要在一块长52m,宽48m的矩形绿地上,修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案.
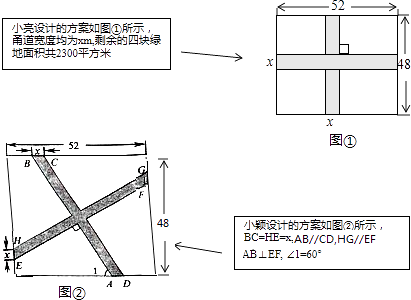
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在y轴的正半轴上,点A在x轴的正半轴上,点C的坐标为(0,8),将△ABC沿直线AB折叠,点C落在x轴的负半轴D(﹣4,0)处.
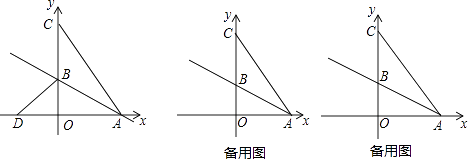
(1)求直线AB的解析式;
(2)点P从点A出发以每秒4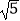 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);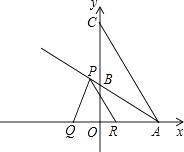
(3)在(2)的条件下,点N是射线AB上一点,以点N为圆心,同时经过R、Q两点作⊙N,⊙N交y轴于点E,F.是否存在t,使得EF=RQ?若存在,求出t的值,并求出圆心N的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
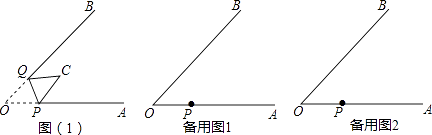
(1)当PC∥QB时,OQ=;
(2)当PC⊥QB时,求OQ的长.
(3)当折叠后重叠部分为等腰三角形时,求OQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格线的交点叫格点,格点
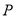 是
是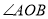 的边
的边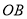 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).
(1)过点
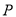 画
画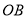 的垂线,交
的垂线,交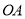 于点
于点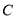 ;
;(2)线段 的长度是点O到PC的距离;
(3)
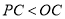 的理由是 ;
的理由是 ; (4)过点C画
 的平行线;
的平行线;
相关试题

