【题目】如图,AB∥DE,AC∥DF,AC=DF,添加下列条件,不能判断 △ABC≌△DEF的是( )
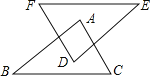
A. EF=BC B. AB=DE C. EF∥BC D. ![]() B=
B=![]() E
E
参考答案:
【答案】A
【解析】
根据全等三角形的判定方法结合所给条件逐项分析即可.
∵AB∥DE,
∴∠1=∠2.
∵AC∥DF,
∴∠1=∠D,
∴∠2=∠D.
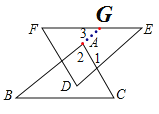
A. 在△ABC和△DEF中,
AC=DF,
EF=BC,
∠2=∠D,
此3个条件符合“SSA”,而“SSA”不能作为全等三角形的判定方法,故A不能判断 △ABC≌△DEF;
B. 在△ABC和△DEF中,
AC=DF,
∠2=∠D,
AB=DE,
∴△ABC≌△DEF(SAS),
故B能判断 △ABC≌△DEF;
C.延长BA交FE于点G.
∵EF∥BC,
∴∠3=∠B.
∵AB∥DE,
∴∠3=∠E,
∴∠B=∠E.
在△ABC和△DEF中,
∠B=∠E,
∠2=∠D,
AC=DF,
∴△ABC≌△DEF(AAS),
故C能判断 △ABC≌△DEF;
D. 在△ABC和△DEF中,
∠B=∠E,
∠2=∠D,
AC=DF,
∴△ABC≌△DEF(AAS),
故D能判断 △ABC≌△DEF;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
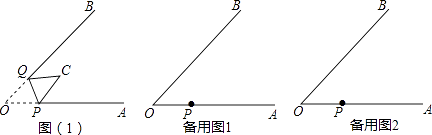
(1)当PC∥QB时,OQ=;
(2)当PC⊥QB时,求OQ的长.
(3)当折叠后重叠部分为等腰三角形时,求OQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格线的交点叫格点,格点
 是
是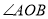 的边
的边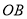 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).
(1)过点
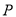 画
画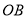 的垂线,交
的垂线,交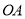 于点
于点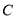 ;
;(2)线段 的长度是点O到PC的距离;
(3)
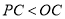 的理由是 ;
的理由是 ; (4)过点C画
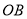 的平行线;
的平行线; -
科目: 来源: 题型:
查看答案和解析>>【题目】a
 b是新规定的一种运算法则:a
b是新规定的一种运算法则:a b=a2+ab,例如3
b=a2+ab,例如3 (﹣2)=32+3×(﹣2)=3.
(﹣2)=32+3×(﹣2)=3.(1)求(﹣3)
 5的值;
5的值;(2)若(﹣2)
 x=6,求x的值;
x=6,求x的值;(3)若3
 (2
(2 x)=﹣4+x,求x的值.
x)=﹣4+x,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D,E的运动时间为t秒,DF⊥BC于F
(1)求证:AE=DF;
(2)如图2,连接EF,
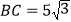
①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由
②连接DE,当△DEF是直角三角形时,求t的值
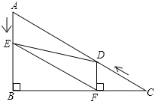

图1 图2 备用图 备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
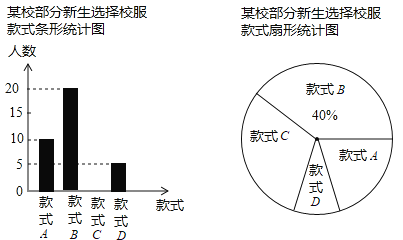
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
相关试题

