搜索
【题目】如图，已知直线y=k1x+b与x轴、y轴相交于P、Q两点，与y=
的图象相交于A（﹣2，m）、B（1，n）两点，连接OA、OB，给出下列结论：①k1k2＜0；②m+
n=0；③S△AOP=S△BOQ；④不等式k1x+b>的解集是x＜﹣2或0＜x＜1，其中正确的结论的序号是_____．
参考答案：
【答案】②③④
【解析】
本题主要考察一次函数的图像与性质、反比例函数的图像与性质以及三角形的基本概念即可求解.
解：①项，由图像得，一次函数的图像单调递减，所以k1<0，反比例函数图像位于第二、四象限，所以k2<0，因此k1k2>0.故①项错误.
②项，将A(-2,m) 代入
中得
，即
，将B（1，n）代入中得k2=n，因此n=-2m，移项得2m+n=0，等式两边同时除2得
.故②项正确.
③项，将A（2，m），B（1，n）代入y=kx1+b，可得
，解得
，将n=-2m代入，得
，对于y=kx1+b，令y=0,可得
，令x=0，可得y=b<0，
∴OP=
，OQ=-b，
∴S△AOP=
，
S△BOQ=
，
因此S△AOP=S△BOQ，故③正确.
④项，不等式
的解集所表示的实际意义为一次函数图像位于反比例函数图像上方时x的取值范围，由图像可知，x的取值范围问x<-2或0<x<1,故④正确.
综上所述，正确结论的序号为②③④.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=
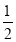∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系．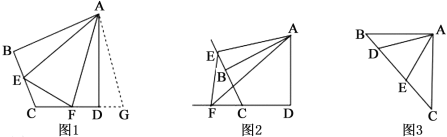
（1）思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合，由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线，易证△AFG≌△AFE，故EF，BE，DF之间的数量关系为__；
（2）类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC延长线上，∠EAF=
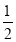∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明．（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°，若BD=1，EC=2，直接写出DE的长为________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y=﹣x+b与反比例函数y=
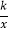（k≠0）的图象相交于点P，则关于x的方程﹣x+b=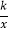的解是_____．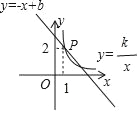
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为 ；
探索：（2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
应用：（3）如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°．若BD＝9，CD＝3，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列从左边到右边的变形，是因式分解的是（ ）
A.y
﹣5y﹣6＝（y﹣6）（y+1）B.a+4a﹣3＝a（a+4）﹣3C.x（x﹣1）＝x
﹣xD.m+n＝（m+n）（m﹣n） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，面积为4的正方形OABC的顶点O与坐标原点重合，边OA、OC分别在x轴、y轴的正半轴上，点B、P都在函数y=
（x＞0）的图象上，过动点P分别作轴x、y轴的平行线，交y轴、x轴于点D、E．设矩形PDOE与正方形OABC重叠部分图形的面积为S，点P的横坐标为m．（1）求k的值；
（2）用含m的代数式表示CD的长；
（3）求S与m之间的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+2与x轴，y轴分别交于点A（﹣1，0）和点B，与反比例函数y=
的图象在第一象限内交于点C（1，n）．（1）求一次函数y=kx+2与反比例函数y=
的表达式；（2）过x轴上的点D（a，0）作平行于y轴的直线l（a＞1），分别与直线y=kx+2和双曲线y=
交于P、Q两点，且PQ=2QD，求点D的坐标．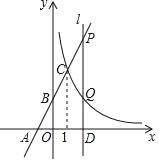
相关试题
