【题目】如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
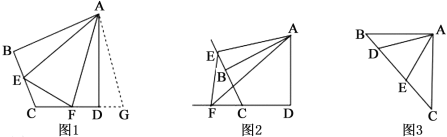
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF之间的数量关系为__;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.
参考答案:
【答案】(1)EF=BE+DF;(2)EF=DFBE;证明见解析;(3)![]() .
.
【解析】
(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,首先证明F,D,G三点共线,求出∠EAF=∠GAF,然后证明△AFG≌△AFE,根据全等三角形的性质解答;
(2)将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',首先证明E',D,F三点共线,求出∠EAF=∠E'AF,然后证明△AFE≌△AFE',根据全等三角形的性质解答;
(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',同(1)可证△AED≌AED',求出∠ECD'=90°,再根据勾股定理计算即可.
解:(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,
∵∠B+∠ADC=180°,
∴∠FDG=180°,即点F,D,G三点共线,
∵∠BAE=∠DAG,∠EAF=![]() ∠BAD,
∠BAD,
∴∠EAF=∠GAF,
在△AFG和△AFE中,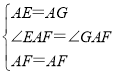 ,
,
∴△AFG≌△AFE,
∴EF=FG=DG+DF=BE+DF;
(2)EF=DFBE;
证明:将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',则△ABE≌ADE',
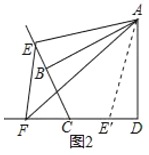
∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∴∠ADE'=∠ADC,即E',D,F三点共线,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠E'AF=∠BAD(∠BAF+∠DAE')=∠BAD(∠BAF+∠BAE)=∠BAD∠EAF=![]() ∠BAD,
∠BAD,
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,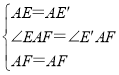 ,
,
∴△AFE≌△AFE'(SAS),
∴FE=FE',
又∵FE'=DFDE',
∴EF=DFBE;
(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',
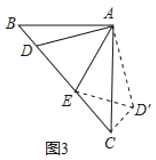
同(1)可证△AED≌AED',
∴DE=D'E.
∵∠ACB=∠B=∠ACD'=45°,
∴∠ECD'=90°,
在Rt△ECD'中,ED'=![]() ,即DE=
,即DE=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.
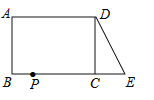
(1)DE的长为 .
(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?
(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.
-
科目: 来源: 题型:
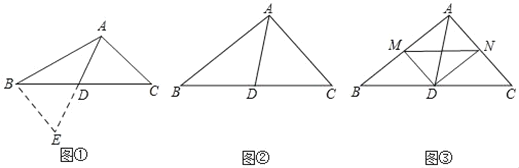
查看答案和解析>>【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=﹣x+b与反比例函数y=
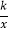 (k≠0)的图象相交于点P,则关于x的方程﹣x+b=
(k≠0)的图象相交于点P,则关于x的方程﹣x+b=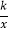 的解是_____.
的解是_____.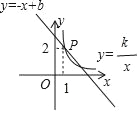
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
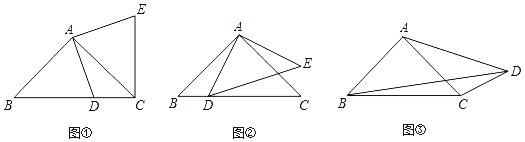
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=
 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+ n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> 的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.
的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.
相关试题

