搜索
【题目】如图，已知一次函数y=﹣x+b与反比例函数y=
（k≠0）的图象相交于点P，则关于x的方程﹣x+b=的解是_____．
参考答案：
【答案】x1=1，x2=2
【解析】
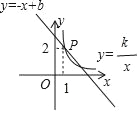
一次函数与反比例函数交与点P，由图已知点P（1,2），将P点在坐标代入一次函数和反比例函数即可求出一次函数与反比例函数的解析式，然后联立一次函数与反比例函数，即可求出关于x的方程﹣x+b=
的解.
解：由题意及图像可知，P的坐标为（1,2），
将P（1,2）带入一次函数y=﹣x+b的解析式，得2= -1+b，解得b=3;
将P（1,2）带入反比例函数y=的解析式，得
，解得k= 2;
∵﹣x+b=.
∴
，
整理有：x2-3x+2=0,解得：x1=1，x2=2.
经检验x1=1，x2=2是方程的解，
故正确答案为：x1=1，x2=2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=3，连接DE．
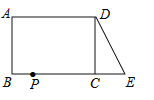
（1）DE的长为 ．
（2）动点P从点B出发，以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒，求当t为何值时，△ABP和△DCE全等？
（3）若动点P从点B出发，以每秒1个单位的速度仅沿着BE向终点E运动，连接DP．设点P运动的时间为t秒，是否存在t，使△PDE为等腰三角形？若存在，请直接写出t的值；否则，说明理由．
-
科目： 来源： 题型：
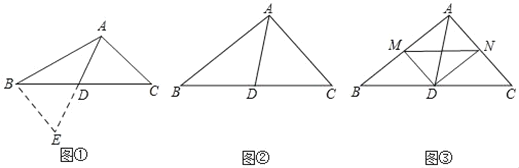
查看答案和解析>>【题目】（问题情境）如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
（1）（问题解决）延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形三边的关系即可判断出中线AD的取值范围是 ．
（反思感悟）解题时，条件中若出现“中点”、“中线”字样，可以考虑构造以该中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同个三角形中，从而解决问题．
（2）（尝试应用）如图②，△ABC中，∠BAC=90°，AD是BC边上的中线，试猜想线段AB，AC，AD之间的数量关系，并说明理由．
（3）（拓展延伸）如图③，△ABC中，∠BAC=90°，D是BC的中点，DM⊥DN，DM交AB于点M，DN交AC于点N，连接MN．当BM=4，MN=5，AC=6时，请直接写出中线AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=
∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系．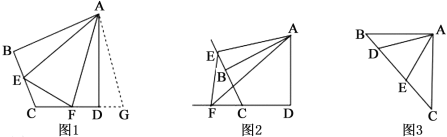
（1）思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合，由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线，易证△AFG≌△AFE，故EF，BE，DF之间的数量关系为__；
（2）类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC延长线上，∠EAF=
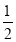∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明．（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°，若BD=1，EC=2，直接写出DE的长为________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：（1）如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为 ；
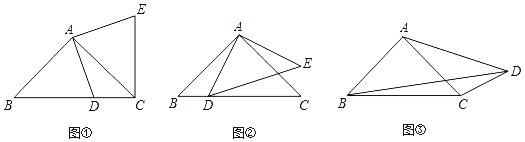
探索：（2）如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
应用：（3）如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°．若BD＝9，CD＝3，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线y=k1x+b与x轴、y轴相交于P、Q两点，与y=
的图象相交于A（﹣2，m）、B（1，n）两点，连接OA、OB，给出下列结论：①k1k2＜0；②m+
n=0；③S△AOP=S△BOQ；④不等式k1x+b>的解集是x＜﹣2或0＜x＜1，其中正确的结论的序号是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列从左边到右边的变形，是因式分解的是（ ）
A.y
﹣5y﹣6＝（y﹣6）（y+1）B.a+4a﹣3＝a（a+4）﹣3C.x（x﹣1）＝x
﹣xD.m+n＝（m+n）（m﹣n）
相关试题
