【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=![]() (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

参考答案:
【答案】(1)k=4;(2)当0<m≤2时,CD=![]() ﹣2;当m>2时,CD=2﹣
﹣2;当m>2时,CD=2﹣![]() ;(3)当0<m≤2时,S=2m
;(3)当0<m≤2时,S=2m
当m>2时,S=![]() ;
;
【解析】
(1)利用正方形的性质的OA=AB=2,则B点则坐标可以求出,将B点坐标代入反比例函数的解析式,即可求出k的值.
(2)分类:P(m,n)在![]() 上,得到mn=4,分以下几类:
上,得到mn=4,分以下几类:
当x>2时,S=AE·PE=![]() ,即可求出n的值;
,即可求出n的值;
当0<x≤2时,S=P'F'·F'C=![]() ,即可求出m的值,
,即可求出m的值,
即可确定P的坐标.
(3)由(2)可以求出x>2与0<x≤2时所对应S的表达式.
(1)∵正方形OABC的面积4,
∴BA=BC=OA=OC=2.
∴点 B(2,2),
∵点B、P都在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=2×2=4,
∴解析式y=![]() ,
,
(2)∵点P在y=![]() 的图象上,且横坐标为m,
的图象上,且横坐标为m,
∴![]() ,
,
当0<m≤2时,CD=![]() ﹣2,
﹣2,
当m>2时,CD=2﹣![]() ,
,
(3)当0<m≤2时,S=2m,
当m>2时,S=2×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
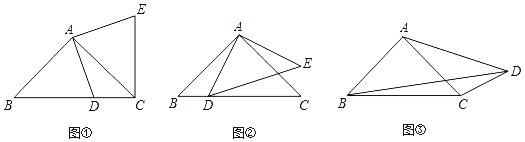
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=
 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+ n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> 的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.
的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,是因式分解的是( )
A.y
 ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3C.x(x﹣1)=x
 ﹣xD.m
﹣xD.m +n
+n =(m+n)(m﹣n)
=(m+n)(m﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=
 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).(1)求一次函数y=kx+2与反比例函数y=
 的表达式;
的表达式;(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=
 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.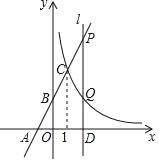
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x﹣2与两坐标轴分别交于点A,C,交y=
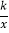 (x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(x>0)于点P,PQ⊥x轴于点Q,CQ=1.(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x﹣2,y=
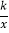 (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.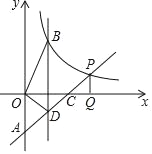
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数
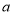 的小数点与算术平方根
的小数点与算术平方根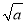 的小数点的移动规律:
的小数点的移动规律: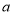
0.0016
0.16
16
1600
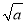
0.04
0.4
(2)根据你发现的规律填空:
①已知
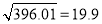 ,则
,则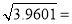 .
.②已知
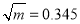 ,
,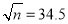 ,则
,则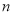 是
是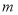 的 倍.
的 倍.
相关试题

