【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.

参考答案:
【答案】(1)证明见解析;(2)DE的长是6;
tan∠AFE的值为![]() ,GD长为
,GD长为![]()
【解析】(1)连接DO,并延长交⊙O于点P,
∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,
∴![]() ,
,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,D是半径OD的外端,
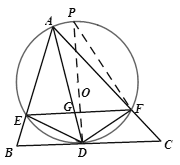
∴BC是⊙O的切线;
(2)∵DP是直径,
∴∠DFP=90°,
∴∠P+∠PDF=90°,
∵∠FDC+∠PDF=90°,
∴∠P=∠FDC=∠DAF=∠DAE,
∵四边形AEDF内接于圆,
∴∠AED=∠DFC,
∴△AED∽△DFC,
∴![]() ,
,
∵![]() ,
,
∴DE=DF,
∴DE2=AE×CF=9×4=36,
∴DE=6;
(3)如图,过E点作EH⊥AD于H点,
∵∠BAC=60°,
∴∠DAE=![]() ∠BAC=30°,
∠BAC=30°,
∴EH=![]() AE=
AE=![]() ,
,
由勾股定理得,AH=![]() ,DH=
,DH=![]() ,
,
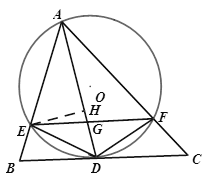
∴tan∠AFE=tan∠ADE=![]() ;
;
AD=![]() +
+![]()
∵![]() ,
,
∴∠EAD=∠DEF,
又∠EDA=∠GDE,
∴△EDA∽△GDE,
∴![]() ,
,
img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/8a524687/SYS201712282305342279559724_DA/SYS201712282305342279559724_DA.018.png" width="189" height="67" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
-
科目: 来源: 题型:
查看答案和解析>>【题目】项式:a,﹣2a2 , 4a3 , ﹣8a4 , …根据你发现的规律,第7个式子是 , 第n个式子是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(2m -3,8),N(m -1,-3),且MN//y轴,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(﹣2,﹣3)关于原点的对称点的坐标是( )
A.(2,3)
B.(﹣2,3)
C.(﹣2,﹣3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣6.5+(﹣3.3)﹣(﹣2.5)﹣(+4.7)
(2)17﹣8÷(﹣22)+4×(﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.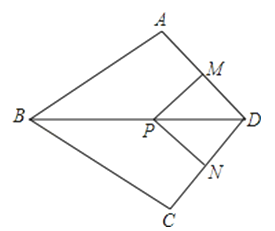
相关试题

