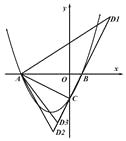
【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为![]() ;
;
(2)满足条件的D点有D1 ![]() ,D2
,D2![]() ,D3(1,4);
,D3(1,4);
(3)满足条件的点P有P![]() 和P′
和P′![]()
【解析】解:(1)依题意得, 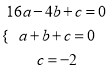 ,解得,
,解得, 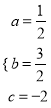 ,
,
 ∴抛物线的解析式为
∴抛物线的解析式为![]() ;
;
(2)①以AD为底时,AB=BD,
设直线BC的解析式为y=kx+b,则![]() ,
,
∴直线BC的解析式为y=2x2,
设D(x,2x2),由(2x2)2+(1x)2=25,解得,
∴D1 ![]() ,D2
,D2![]() ,
,
②以BD为底时,AB=AD,
B点关于AC的对称点D3(1,4),
综上所述,满足条件的D点有D1 ![]() ,D2
,D2![]() ,D3(1,4);
,D3(1,4);
∵AC2+BC2=AB2,
∴∠ACB=90°,
当P点在第三象限时,
设(2)中AD3交抛物线![]() 于P点,
于P点,
过P点作PQ⊥AC于Q点,由(2)可知∠BAC=∠PAC,
∠ACB=∠AQP, ∴△APQ∽△ABC,
设直线AP的解析式为y=mx+n,由![]() ,解得,
,解得, 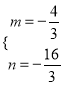

∴直线AP的解析式为![]() ,
,
由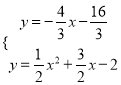 ,解得,
,解得, 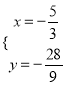 或
或![]() (舍去),
(舍去),
∴P![]() ;
;
当P点在第三象限时,
过A点作AP′⊥AD3,交抛物线![]() 于P′点,
于P′点,
过P′点作P′Q′⊥AC于Q′点,由(2)可知∠BAC=∠AP′Q′,
∠ACB=∠AQ′P′, ∴△P′AQ′∽△ABC,
易得直线AP′的解析式为![]() ,
,
同(3)过程可求P′![]() ,
,
综上,满足条件的点P有P![]() 和P′
和P′![]()
此题解法不唯一,请酌情评分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象经过点(-1,2),求二次函数y=ax2的解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】项式:a,﹣2a2 , 4a3 , ﹣8a4 , …根据你发现的规律,第7个式子是 , 第n个式子是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(2m -3,8),N(m -1,-3),且MN//y轴,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点(﹣2,﹣3)关于原点的对称点的坐标是( )
A.(2,3)
B.(﹣2,3)
C.(﹣2,﹣3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣6.5+(﹣3.3)﹣(﹣2.5)﹣(+4.7)
(2)17﹣8÷(﹣22)+4×(﹣3)
相关试题

