【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.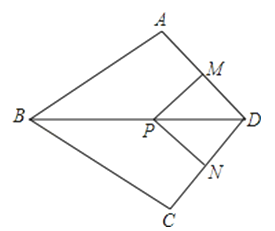
参考答案:
【答案】证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中, ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.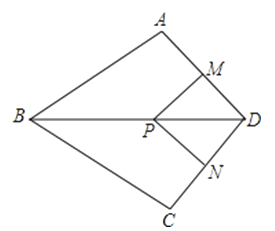
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点(﹣2,﹣3)关于原点的对称点的坐标是( )
A.(2,3)
B.(﹣2,3)
C.(﹣2,﹣3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣6.5+(﹣3.3)﹣(﹣2.5)﹣(+4.7)
(2)17﹣8÷(﹣22)+4×(﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,王老师出了这样一道题:“已知a=2019-2,b=(-2018)3,求代数式(a-3b)2-2a(a-7b)+(a+b)(a-9b)+1的值.”小明觉得计算量太大了,请你来帮他解决,并写出具体过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(4a+3a2)﹣1﹣3a3﹣(a﹣3a3),其中a=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据﹣2、1、1、0、2、1.这组数据的众数和中位数分别是( )
A. ﹣2、0B. 1、0C. 1、1D. 2、1
相关试题

