【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1. 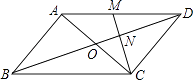
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
参考答案:
【答案】
(1)解:∵平行四边形ABCD,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴ ![]() ,
,
∵M为AD中点,
∴MD= ![]() AD=
AD= ![]() BC,即
BC,即 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即BN=2DN,
,即BN=2DN,
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1),
解得:x=3,
∴BD=2x=6;
(2)解:∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND= ![]() S△CND=1,S△BNC=2S△CND=4.
S△CND=1,S△BNC=2S△CND=4.
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6
∴S四边形ABNM=S△ABD﹣S△MND=6﹣1=5.
【解析】(1)由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;(2)由相似三角形相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND , 最后由S四边形ABNM=S△ABD﹣S△MND求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学实验室:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是 ,若AB=2,那么x为 ;
(3)当x是 时,代数式
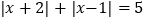 ;
;(4)若点A表示的数-1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,PQ=1?(请写出必要的求解过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合中:
-6, 9.3, -
 , 15, 0, -0.33, -0.333…, 1.41421356, -3
, 15, 0, -0.33, -0.333…, 1.41421356, -3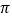 , 3.3030030003…, -3.1415926.
, 3.3030030003…, -3.1415926.正数集合:{ … }
负数集合: { … }
有理数集合: { … }
无理数集合: { … }
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
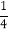 +
+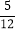
 )×(-60) (2) (-
)×(-60) (2) (- )×(-3
)×(-3 )÷(-1
)÷(-1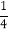 )÷3;
)÷3;(3) (-5)×(-3
 )+(-7)×(-3
)+(-7)×(-3 )+12×(-3
)+12×(-3 ) (4) 19
) (4) 19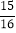 ×(-8)
×(-8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD.
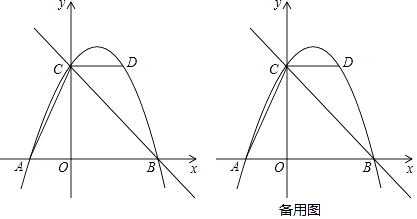
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
相关试题

