【题目】数学实验室:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是 ,若AB=2,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数-1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,PQ=1?(请写出必要的求解过程)
参考答案:
【答案】(1)3,4;(2)∣x+2∣,0或-4;(3)-3或2;(4)4.5或5.5秒.
【解析】
(1)根据数轴上两点间的距离的求解方法列式计算即可得解;
(2)根据数轴上两点间的距离等于这两个数的差的绝对值列式即可;
(3)根据代数式│x+2│+│x-1│=5列出x的取值范围,即可求出x的值;
(4)点P和点Q作追击运动,设运动时间为t,根据路程的差为10列方程求解.
(1)|25|=3,
|1(3)|=4;
(2)|x(2)|=|x+2|;当AB=2,则|x+2|=2,x=0或x=-4;
(3)∵│x+2│+│x-1│=5,
则x在﹣2的左边或1的右边,
设x到﹣2或1的距离为a,
2a+3=5,
解得:a=1.
则x=-3或x=2.
(4)设运动时间为t,根据路程的差为10,
3t-t=9或3t-t=11
解得:t=4.5或5.5秒.
-
科目: 来源: 题型:
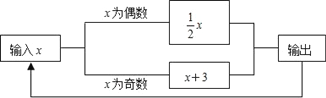
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察下列图形与等式的关系,并填空:
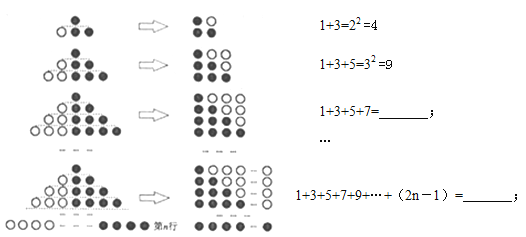
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+203= ;
②计算:101+103+105+…+199;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
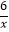 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点. 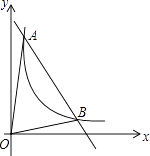
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<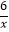 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的集合中:
-6, 9.3, -
 , 15, 0, -0.33, -0.333…, 1.41421356, -3
, 15, 0, -0.33, -0.333…, 1.41421356, -3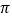 , 3.3030030003…, -3.1415926.
, 3.3030030003…, -3.1415926.正数集合:{ … }
负数集合: { … }
有理数集合: { … }
无理数集合: { … }
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
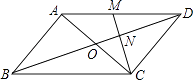
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
相关试题

