【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD. 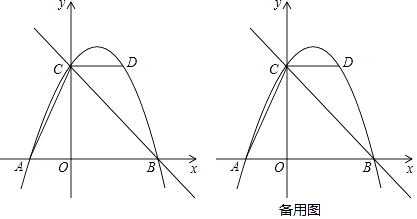
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),
∴设抛物线的解析式为y=a(x﹣x1)(x﹣x2),
∴y=a(x+2)(x﹣4),
∴﹣8a=4,
∴a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣ ![]() x2+x+4
x2+x+4
(2)解:①当点E在直线CD的抛物线上方,记E′,连接CE′,过点E′作E′F′⊥CD,垂足为F′,
由(1)得OC=4,
∵∠ACO=∠E′OF′,
∴tan∠ACO=tan∠E′CF′,
∴ ![]() =
= ![]() =
= ![]() ,
,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4),
∵点E′在抛物线上,
∴﹣ ![]() (2h)2+2h+4=h+4,
(2h)2+2h+4=h+4,
∴h1=0(舍去),h2= ![]() ,
,
∴E′(1, ![]() );
);
②当点E在直线CD的抛物线下方;
同①的方法得,E(3, ![]() ),
),
综上,点E的坐标为(1, ![]() ),(3,
),(3, ![]() ).
).
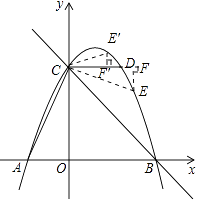
【解析】(1)设抛物线的解析式为y=a(x﹣x1)(x﹣x2),再把点代入即可得出解析式;(2)分两种情况:①当点E在直线CD的抛物线上方;②当点E在直线CD的抛物线下方;连接CE,过点E作EF⊥CD,再由三角函数得出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
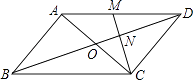
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 +
+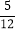
 )×(-60) (2) (-
)×(-60) (2) (- )×(-3
)×(-3 )÷(-1
)÷(-1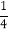 )÷3;
)÷3;(3) (-5)×(-3
 )+(-7)×(-3
)+(-7)×(-3 )+12×(-3
)+12×(-3 ) (4) 19
) (4) 19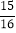 ×(-8)
×(-8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明有5张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题:
(1)从中取出3张卡片,使这3张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?

相关试题

