【题目】已知点![]() 为直线
为直线![]() 上的一点,
上的一点,![]() 为直角,
为直角,![]() 平分
平分![]() .
.
(1)如图1,若![]() ,则
,则![]() ______°.
______°.
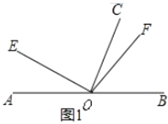
(2)如图1,若![]() ,求
,求![]() 的度数.(用含
的度数.(用含![]() 的代数式表示)
的代数式表示)
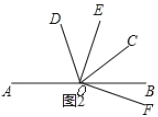
(3)如图2,若![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)22.5(2)![]() (3)160
(3)160
【解析】
(1)由∠AOE=45°,可以求得∠BOE=135°,再由OC平分∠BOE,可求得∠EOC=67.5°,∠EOF为直角,所以可得∠COF=∠EOF∠EOC=22.5°;
(2)由(1)的方法即可得到∠COF=![]() °;
°;
(3)先设∠BOF为x°,再根据角的关系得出方程,解答后求出n的值即可.
解:(1)∵∠AOE=45°,
∴![]() =135°,
=135°,
∵![]() 平分
平分![]() ,
,
∴∠EOC=67.5°
∵![]() 为直角,
为直角,
∴∠COF=∠EOF∠EOC=22.5°;
(2))∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]()
∵![]() 为直角,
为直角,
∴![]()
(3)设![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 平分
平分![]() ,
,
则可得:![]() ,
,
![]()
解得:![]() ,
,
所以可得:![]() ,
,
![]() ,
,
故![]() 的值是160.
的值是160.
故答案为:160
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 在平面直角坐标系中,
在平面直角坐标系中,  ,
, ,把矩形
,把矩形 沿直线
沿直线 对折使点
对折使点 落在点
落在点 处,直线
处,直线 与
与 的交点分别为
的交点分别为 ,点
,点 在
在 轴上,点
轴上,点 在坐标平面内,若四边形
在坐标平面内,若四边形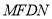 是菱形,则菱形
是菱形,则菱形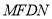 的面积是( )
的面积是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“元旦”期间,七(1)班小明,小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:

(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,用哪种方式购票省钱?请说明理由.
(3)正要购票时,小明发现七(2)班的小张等10名同学和他们的7名家长共17人也来购票,为了节省费用,经协商,他们决定一起购票,请你为他们设计最省钱的购票方案,并求出此时的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:
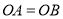 ,
, .
.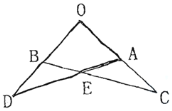
(1)请找出图中一对全等的三角形,并说明理由;
(2)若
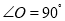 ,
,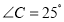 ,求
,求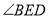 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年全国中小学生“安全教育日”主题是“珍爱生命,安全伴我行”.小明骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
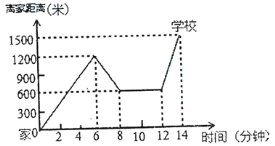
(1)小明家到学校的路程是________米;小刚在书店停留了________分钟;
(2)本次上学途中,小明全程一共用了________分钟;一共骑行了________米.
(3)我们认为骑单车的速度超过300米/分就超过了安全限度,在整个上学的途中哪个时间段小明骑车速度最快?速度在安全限度内吗?请给小明提一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,OA=3,OC=4
 ,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.(1)求直线AC的函数解析式;
(2)设点
 ,记平行四边形ABCD的面积为
,记平行四边形ABCD的面积为 ,请写出
,请写出 与
与 的函数关系式,并求当BD取得最小值时,函数
的函数关系式,并求当BD取得最小值时,函数 的值;
的值;(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决后面的问题.
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707-1783)才发现指数与对数之间的联系.我们知道,n个相同的因数a相乘
 记为
记为 ,如
,如 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为 ,即
,即 .
.一般地,若
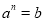 (
( 且
且 ,
, ),则n叫做以a为底b的对数,记为
),则n叫做以a为底b的对数,记为 ,即
,即 .如
.如 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为 ,即
,即 .
.(1)计算下列各对数的值:
 ________,
________, ________,
________, ________;
________;(2)通过观察(1)中三数
 、
、 、
、 之间满足的关系式是________;
之间满足的关系式是________;(3)拓展延伸;下面这个一般性的结论成立吗?我们来证明
 (
( 且
且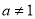 ,
, ,
, )
)证明:设
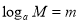 ,
, ,
,由对数的定义得:
 ,
, ,
,∴
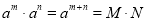 ,
,∴
 ,
,又∵
 ,
, ,
,∴
 (
( 且
且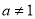 ,
, ,
, ).
).(4)仿照(3)的证明,你能证明下面的一般性结论吗?
 (
( 且
且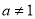 ,
, ,
, ).
).(5)计算:
 的值为________________.
的值为________________.
相关试题

