搜索
【题目】已知抛物线y＝ax2＋b x＋c经过A，B，C三点，当x≥0时，其图象如图所示．
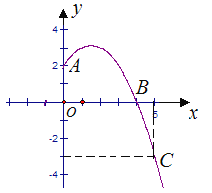
（1）求抛物线的解析式，写出抛物线的顶点坐标；
（2）画出抛物线y＝ax2＋b x＋c当x＜0时的图象；
（3）利用抛物线y＝ax2＋b x＋c，写出x为何值时，y＞0．
参考答案：
【答案】（1）抛物线y ＝
顶点（
，
）（2）略（3） 当－1＜x＜4时， y >0
【解析】试题分析：本题的关键是求出抛物线的解析式，在题目给出的图象中可得出A、B、C三点的坐标，可用待定系数求出抛物线的解析式，进而可画出x＜0时抛物线的图象，以及y＞0时x的取值范围．
解：（1）由图象，可知A（0，2），B（4，0），C（5，﹣3），
得方程组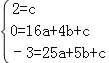
．
解得a=﹣
，b=
，c=2．
∴抛物线的解析式为y=﹣x2+x+2．
顶点坐标为（，
）．
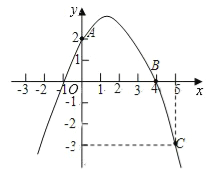
（2）所画图如图．
（3）由图象可知，当﹣1＜x＜4时，y＞0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A，B，C，其中AB=2，BC=1，如图所示，设点A，B，C所对应数的和是p.
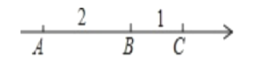
(1)若以B为原点，写出点A，C所对应的数，并计算p的值；若以C为原点，p又是多少?
(2)若原点O在图中数轴上点C的右边，且CO=28，求p.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线过A(－1，0)，B(3，0)两点，与y轴交于C点，且BC=3
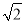，则这条抛物线的解析式为 ( )A. y=－x2+2x+3 B. y＝x2－2x－3
C. y=x2+2x―3或y＝－x2+2x+3 D. y=－x2+2x+3或y＝x2－2x－3
-
科目： 来源： 题型：
查看答案和解析>>【题目】用配方法把二次函数y＝l+2x－x2化为y＝a(x－h)2+k的形式，作出它的草图，回答下列问题．
(1)求抛物线的顶点坐标和它与x轴的交点坐标；
(2)当x取何值时，y随x的增大而增大?
(3)当x取何值时，y的值大于0?
-
科目： 来源： 题型：
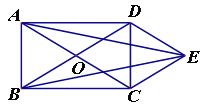
查看答案和解析>>【题目】如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD.
（1）求证：四边形OCED为菱形；
（2）连接AE、BE，AE与BE相等吗？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】―抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．
(1)求该抛物线的解析式；
(2)求该抛物线的顶点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕点B逆时针旋转得到的．点O′在x轴的正半轴上，点B的坐标为(1，3)．
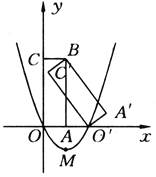
(1)如果二次函数y＝ax2+bx+c（a≠0)的图象经过O，O′两点，且图象顶点M的纵坐标为－l，求这个二次函数的解析式；
(2)在(1)中求出的二次函数图象对称轴的右侧，是否存在点P，使得△POM为直角三角形?若存在，求出点P的坐标和△POM的面积；若不存在，请说明理由；
(3)求边C′O′所在直线的解析式．
相关试题
