【题目】如图所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
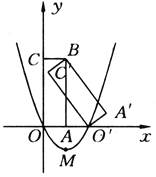
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
参考答案:
【答案】(1) y=x2-2x(2)1(3)y=![]()
【解析】分析:(1)连接BO,B![]() 则B0=B
则B0=B![]() ,求出
,求出![]() M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知
M点坐标,列出方程组求出未知数的值,进而求出二次函数的解析式;(2)设存在满足题设条件的点P(x,y),连接OM,PM,OP,过P作PN⊥x轴,求出P点坐标和△POM的面积.(3)已知![]() (2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
(2,0),点D的横坐标为1,由相似关系求其纵坐标,用待定系数法求解析式.
本题解析:(1)如图2-83所示,连接BO,BO′,则BO=BO′.∵BA⊥OO′,∴AO=AO′.∵B(1,3),∴O′(2,0),M(1,-1),∴ 解得
解得 ∴所求二次函数的解析式为y=x2-2x.
∴所求二次函数的解析式为y=x2-2x.
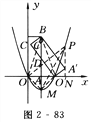
(2)假设存在满足题设条件的点P(x,y).连接OM,PM,OP,过P作PN⊥x轴于N,则∠POM=90°.∵M(1,-1),A(1,0),AM=OA,∴∠NOA=45°,∴∠PON=45°,∴ON=NP,即x=y.∵P(x,y)在二次函数y=x2-2x的图象上,∴x=x2-2x,解得x=0或x=3.∵P(x,y)在对称轴的右侧,∴x>1,∴x=3,y=3,即P(3,3)是所求的点.连接MO′,显然△OMO′为等腰直角三角形,∴点O′(2,0)也是满足条件的点,∴满足条件的点是P(2,0)或P(3,3),∴OP=3![]() ,OM=
,OM=![]() ,∴S△POM=
,∴S△POM=![]() OP·OM=3或S△POM=
OP·OM=3或S△POM=![]() OM·O′M=1.
OM·O′M=1.
(3)设AB与C′O′的交点为D(1,y),显然Rt△DAO′≌Rt△DC′B.在Rt△DAO′中,AO′2+AD2=O′D2,即1+y2=(3-y)2,解得y=![]() ,∴D(1,
,∴D(1, ![]() ).设边C′O′所在直线的解析式为y=kx+b,则
).设边C′O′所在直线的解析式为y=kx+b,则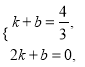 解得
解得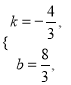 ∴所求直线的解析式为y=
∴所求直线的解析式为y=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
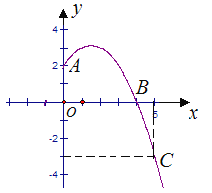
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
-
科目: 来源: 题型:
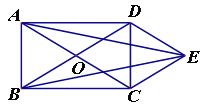
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】―抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,点E是AC的一点,连接EB,过点A做AM⊥BE,垂足为M,AM与BD相交于点F.
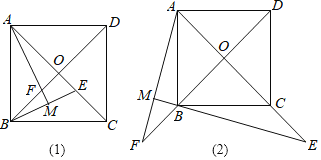
(1)猜想:如图(1)线段OE与线段OF的数量关系为 ;
(2)拓展:如图(2),若点E在AC的延长线上,AM⊥BE于点M,AM、DB的延长线相交于点F,其他条件不变,(1)的结论还成立吗?如果成立,请仅就图(2)给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
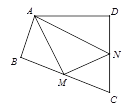
查看答案和解析>>【题目】四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;

(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
相关试题

