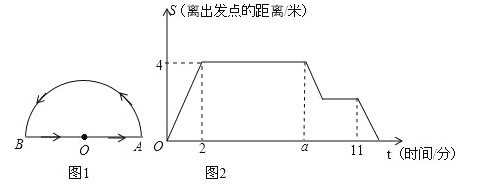
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 米,a= .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
参考答案:
【答案】(1)4,8;(2)s=2t;(3)①2米;②12分钟.
【解析】试题分析:(1)根据圆上的点到圆心的距离等于半径可知S开始不变时的值即为花坛的半径,然后求出蚂蚁的速度,再根据时间=路程÷速度计算即可求出a;
(2)设s=kt(k≠0),然后利用待定系数法求正比例函数解析式解答;
(3)①根据蚂蚁吃食时离出发点的距离不变判断出蚂蚁在BO段,再求出蚂蚁从B爬到吃食时的时间,然后列式计算即可得解;
②求出蚂蚁吃完食后爬到点O的时间,再加上11计算即可得解.
试题解析:(1)由图可知,花坛的半径是4米,
蚂蚁的速度为4÷2=2米/分,
a=(4+4π)÷2=(4+4×3)÷2=8;
故答案为:4,8;
(2)设s=kt(k≠0),
∵函数图象经过点(2,4),
∴2k=4,
解得k=2,
∴s=2t;
(3)①∵沿途只有一处食物,
∴蚂蚁只能在BO段吃食物,11﹣8﹣2=1,
∴蚂蚁从B爬1分钟找到食物,
4﹣1×2=2(米),
∴蚂蚁停下来吃食的地方距出发点2米;
②2÷2=1(分钟),
11+1=12(分钟),
∴蚂蚁返回O的时间为12分钟.
-
科目: 来源: 题型:
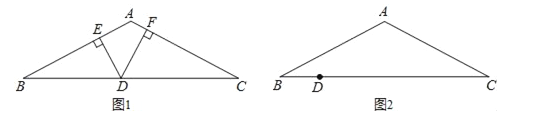
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )

A.4
B.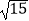
C.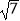
D.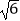
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3是关于x的一元二次方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( ) ①﹣(﹣3)的相反数是﹣3
②近似数1.900×105精确到百位
③代数式|x+2|﹣3的最小值是0
④两个六次多项式的和一定是六次多项式.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,D为AB的中点,E为AC的中点,∠A=30°,AB=12,则DE的长度是 .
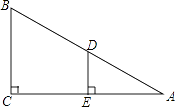
-
科目: 来源: 题型:
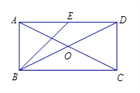
查看答案和解析>>【题目】如图,在矩形
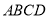 中,对角线
中,对角线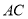 ,
, 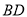 相交于点
相交于点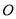 ,
, 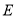 是边
是边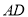 的中点,且
的中点,且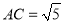 ,
, 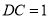 .
.
(1)求证:
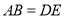 ;
;(2)求
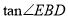 的值.
的值.
相关试题

