【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由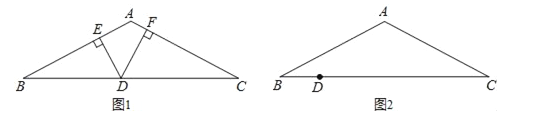
参考答案:
【答案】(1)答案见解析;(2)BG=DE+DF;(3)答案见解析;(4)成立.
【解析】试题分析:(1)按要求作出AC边上的高BG即可;
(2)连接AD,分别求出△ABD、△ADC与△ABC的面积,进而可得出结论;
(3)根据(2)中的过程即可得;
(4)根据(2)中的证明过程可得出结论.
试题解析:(1)如图所示:
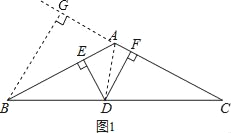
(2)BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() AC(DE+DF),
AC(DE+DF),
∵BG⊥AC,
∴S△ABC=![]() ACBG,
ACBG,
∴BG=DE+DF,
故答案为:BG=DE+DF;
(3)由(2)可知,S△ADC=![]() ACDF,S△ABD=
ACDF,S△ABD=![]() ABDE,
ABDE,
∴S△ABC=![]() ACDF+
ACDF+![]() ABDE,
ABDE,
S△ABC还可以表示为![]() ACBG,
ACBG,
故答案为: ![]() ACDF,
ACDF, ![]() ABDE,
ABDE, ![]() ACDF+
ACDF+![]() ABDE,
ABDE, ![]() ACBG;
ACBG;
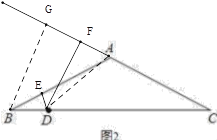
(4)拓展结论仍然成立,即BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() AC(DE+DF),
AC(DE+DF),
∵BG⊥AC,
∴S△ABC=![]() ACBG,
ACBG,
∴BG=DE+DF.
-
科目: 来源: 题型:
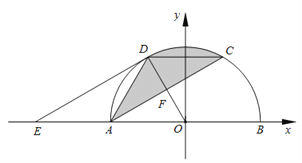
查看答案和解析>>【题目】如图,
 为
为 的直径,
的直径,  为弦
为弦 的中点,连接
的中点,连接 并延长交
并延长交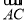 于点
于点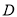 ,过点
,过点 作
作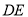 ∥
∥ ,交
,交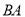 的延长线于点
的延长线于点 ,连接
,连接 ,
,  .
.
(1)求证:
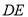 是⊙
是⊙ 的切线;
的切线;(2)若
 时,
时,①求图中阴影部分的面积;
②以
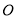 为原点,
为原点,  所在的直线为
所在的直线为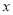 轴,直径
轴,直径 的垂直平分线为
的垂直平分线为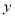 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段 上求一点
上求一点 ,使得直线
,使得直线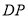 把阴影部分的面积分成
把阴影部分的面积分成 的两部分.
的两部分. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在“校园读书节”活动中,购买甲、乙两种图书共100本作为奖品,已知乙种图书的单价比甲种图书的单价高出50%.同样用360元购买乙种图书比购买甲种图书少4本.
(1)求甲、乙两种图书的单价各是多少元;
(2)如果购买图书的总费用不超过3500元,那么乙种图书最多能买多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是方程x 2+3x-6=0的根,则代数式3a 2+9a+12的值为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )

A.4
B.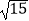
C.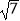
D.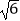
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3是关于x的一元二次方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
-
科目: 来源: 题型:
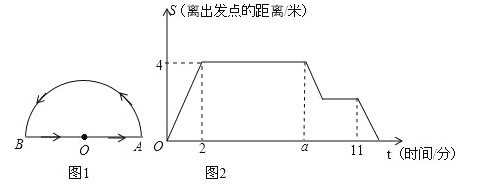
查看答案和解析>>【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)请直接写出:花坛的半径是 米,a= .
(2)当t≤2时,求s与t之间的关系式;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方,离出发点的距离.
②蚂蚁返回O的时间.(注:圆周率π的值取3)
相关试题

