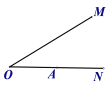
【题目】如图,两个30°的角BAC与角MON,顶点A在射线ON上某处,现保持角MON不动,将角BAC绕点A以每秒15°的速度顺时针旋转,边AB、AC分别与边OM交于点P、Q,当AC∥OM时,交点Q消失旋转结束。设运动时间为t秒(t>0).



(1)当t=2秒时,OP:PQ= ;
(2)在运动的过程中,△APQ能否成为等腰三角形?若能,请利用备用图,直接写出此时的运动时间;
(3)在(2)中判断△OAQ的形状,并选择其中的一个说明理由.
参考答案:
【答案】(1)2:1;
(2)当t=3s或6s时,△APQ为等腰三角形;
(3)△OAQ为等腰三角形,理由见解析.
【解析】
(1)当t=2秒时,∠PAO=30°,∠PQA=90°,根据等角对等边定理和30度角所对直角边等于斜边的一半可得出结论;
(2)先求出t的取值范围,然后分三种情况讨论,当△APQ为等腰三角形时∠PAO的大小,并进而得到t的值;
(3)由(2)得到t的值,代入求得△OAQ的内角度数,从而判断△OAQ的形状。
解:(1)如图1,

当t=2秒时,∠PAO=30°,
∵∠MON=∠BAC=30°
∴∠PAO=∠MON, ∠PQA=90°,
∴OP=AP,PQ=![]() AP,
AP,
∴OP:PQ= 2:1;
故答案为:2:1;
(2)当AC∥OM时,∠NAC=∠O=![]() ,
,
∴∠OAB=![]()
∴t=![]()
∴0<t<8,
分三种情况: AP=AQ 、AP=PQ和QP=QA,
①当AP=AQ时,
∠APQ=∠AQP=![]()
∴∠PAO=∠APQ-∠O=![]()
∴t=![]() ;
;
②当AP=PQ时,
∠APQ=![]()
∴∠PAO=∠APQ-∠O=![]()
∴t=![]() ;
;
③当QP=QA时,
∠APQ=∠PAQ=![]()
∴∠PAO=∠APQ-∠O=![]()
即t=0s(舍去)
综上所述,当t=3s或6s时,△APQ为等腰三角形;
(3)当t=3s或6s时,△OAQ为等腰三角形,
理由是:
当t=3s时,∠OAP=45°,∠PAQ=30°,
∴∠OAQ=75°,
又∠AQP=75°,
∴OA=OQ,即△APQ为等腰三角形.
当t=6s时,∠OAP=90°,∠PAQ=30°,
∴∠OAQ=120°,
又∠AOQ=30°,
∴∠OQA=30°
∴OA=AQ,即△APQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正方形
中,正方形 中心在原点,且顶点
中心在原点,且顶点 的坐标为
的坐标为 .动点
.动点 分别从点
分别从点 同时出发,绕着正方形的边按顺时针方向运动,当
同时出发,绕着正方形的边按顺时针方向运动,当 点回到
点回到 点时两点同时停止运动,运动时间为
点时两点同时停止运动,运动时间为 秒.连接
秒.连接 ,线段
,线段 、
、 与正方形的边围成的面积较小部分的图形记为
与正方形的边围成的面积较小部分的图形记为 .
.(1)请写出
 点的坐标.
点的坐标.(2)若
 的速度均为1个单位长度秒,试判断在运动过程中,
的速度均为1个单位长度秒,试判断在运动过程中, 的面积是否发生变化,如果不变求出该值,如果变化说明理由.
的面积是否发生变化,如果不变求出该值,如果变化说明理由.(3)若
 点速度为2个单位长度秒,
点速度为2个单位长度秒, 点为1个单位长度/秒,当
点为1个单位长度/秒,当 的面积为
的面积为 时,求
时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
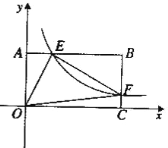
查看答案和解析>>【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数
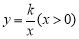 的图象与边BC交于点F。
的图象与边BC交于点F。【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求
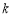 的值:
的值:【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=
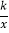 的图象上,OA=2,OC=6,则正方形ADEF的边长为______.
的图象上,OA=2,OC=6,则正方形ADEF的边长为______.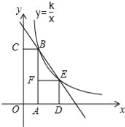
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,点C是OA的中点,过点C作CD⊥OA于C交一次函数图象于点D,P是OB上一动点,则PC+PD的最小值为( )

A.4B.
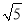 C.2
C.2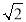 D.2
D.2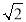 +2
+2
相关试题

