搜索
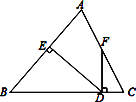
【题目】如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．
⑴若∠AFD=155°，求∠EDF的度数；
⑵若点F是AC的中点，求证：∠CFD=
∠B．
参考答案：
【答案】（1）50°；（2）见解析
【解析】试题分析：⑴根据等腰三角形的性质、三角形的内角和定理与四边形的内角和为360°，可求得所求角的度数.
⑵连接BF，根据三角形内角和定理与等腰三角形三线合一，可知
.
试题解析：⑴ ∵∠AFD=155°，∴∠DFC=25°，∵DF⊥BC，DE⊥AB，
∴∠FDC=∠AED=90°，
在Rt△EDC中，∴∠C=90°﹣25°=65°，
∵AB=BC，∴∠C=∠A=65°，
∴∠EDF=360°﹣65°﹣155°﹣90°=50°．
⑵ 连接BF，∵AB=BC，且点F是AC的中点，
∴BF⊥AC，
，
∴∠CFD+∠BFD=90°，∠CBF+∠BFD=90°，
∴∠CFD=∠CBF，
∴．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB，BC上分别找一点E,F,使△DEF的周长最小，此时，∠EDF=______。（用含α的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
在数轴上的位置如图所示，所对应的点分别为
．
（1）在数轴上表示
的点与表示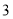
的点之间的距离为 ；由此可得点
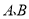之间的距离为 （2）化简：
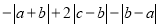
（3）若
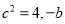的倒数是它本身，
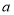的绝对值的相反数是
，
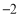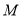是数轴上表示
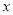的一点，且
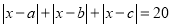，求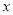所表示的数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的三个顶点坐标分别为A（﹣1，﹣2），B（﹣1，﹣4），C（2，﹣3）．
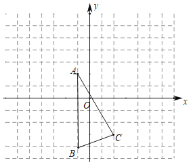
（1）将△ABC先向右平移4个单位，再向上平移6个单位，得到△A1B1C1，作出△A1B1C1，线段AC在平移过程中扫的面积为 ；
（2）作出△A1B1C1关于y轴对称的图形△A2B2C2，则坐标C2为 ；
（3）若△ABD与△ABC全等，则点D的坐标为 （点C与点D不重合）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑，每台售价4000元．为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
（1）有几种进货方案？
（2）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a元，要使（2）中所有方案获利相同，a值应是多少？ 若考虑投入成本最低，则应选择哪种进货方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，∠BAC=60°，点0是△ABC内一点，△AB0
△ACD，连接OD.（1）求证△AOD为等边三角形。
（2）如图2，连接OC，若∠BOC=130°，∠AOB=
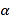.①求∠OCD的度数
②当△OCD是等腰三角形时，求∠
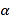的度数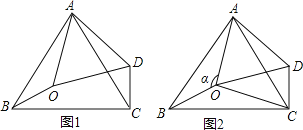
、 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上A，B两点对应的数分别为a，b，且a，b满足|a+20|=﹣（b﹣13）2，点C对应的数为16，点D对应的数为﹣13．
（1）求a，b的值；
（2）点A，B沿数轴同时出发相向匀速运动，点A的速度为6个单位/秒，点B的速度为2个单位/秒，若t秒时点A到原点的距离和点B到原点的距离相等，求t的值；
（3）在（2）的条件下，点A，B从起始位置同时出发．当A点运动到点C时，迅速以原来的速度返回，到达出发点后，又折返向点C运动．B点运动至D点后停止运动，当B停止运动时点A也停止运动．求在此过程中，A，B两点同时到达的点在数轴上对应的数．
相关试题
