【题目】C,D两城蔬菜紧缺,A,B两城决定支援,A城有蔬菜20吨,B城有蔬菜40吨,C城需要蔬菜16吨,D城需要蔬菜44吨,已知A到C,D的运输费用分别为200元/吨,220元/吨,B到C,D的运输费用分别为300元/吨,340元/吨,规定A向C城运的吨数不小于B向C城运的吨数,设A城向C城运x吨,请回答下列问题:
(1)根据题意条件,填写下列表格:

(2)设总费用为y(元),求出y(元)与x(吨)的函数关系式,并写出x的取值范围;
(3)怎样调运货物能使总费用最少?最少费用是多少?
参考答案:
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ;(2)
;(2)![]() ,
,![]() ;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
【解析】
(1)用C城需要蔬菜的吨数减去x可得①的值;用A城共有的蔬菜吨数减去x可得②的值;用B城共有的蔬菜吨数减去①的值可得③的值;
(2)在(1)的基础上,根据题干已知的运输费用列出等式即可得;再根据“A向C城运的吨数不小于B向C城运的吨数”以及①、②的值均为非负数即可得求出x的取值范围;
(3)根据(2)的结论,利用一次函数的性质即可得.
(1)由题意得:①的值为![]() ;②的值为
;②的值为![]() ;③的值为
;③的值为![]()
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由题意得:![]()
整理得:![]()
![]() ①、②的值均为非负数
①、②的值均为非负数
![]()
解得![]()
又![]() A向C城运的吨数不小于B向C城运的吨数
A向C城运的吨数不小于B向C城运的吨数
![]()
解得![]()
综上,x的取值范围是![]() ;
;
(3)由(2)知,![]() ,且
,且![]()
由一次函数的性质可知,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
则当![]() 时,y取得最小值,最小值为
时,y取得最小值,最小值为![]() (元)
(元)
此时,![]() ,
,![]() ,
,![]()
答:当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国庆放假时,小明一家三口准备驾驶小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,先向东走了6千米到超市买东西,然后再向东走了1.5千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)若小轿车每千米耗油0.08升,求小明一家从出发到返回家所经历路程小车的耗油量.
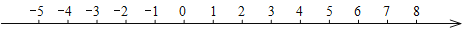
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,|a|表示a到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a、b表示,那么AB=|a-b|.(思考一下,为什么?),利用此结论,回答以下问题:
(1)数轴上表示2和5的两点之间的距离是_____.数轴上表示-2和-5的两点之间的距离___.数轴上表示1和-3的两点之间的距离是_____;
(2)数轴上表示x和-1的两点A、B之间的距离是___________;
如果|AB|=2,x的值为_____;
(3)说出|x+1|+|x+2|表示几何的意义_,该代数式的最小值是:_____;
(4)求|x-1|+|x-2|+|x-3|+...+|x-2019|的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,A1、P两点表示的数分别为1、3,A1、A2关于O对称,A2、A3关于点P对称,A3、A4关于点O对称,A4、A5关于点P对称…依次规律,则点A15表示的数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入它所属的集合内:将下列各数填入相应的括号内:
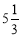 ,
,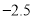 ,
,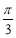 ,
,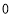 ,
,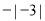 ,
,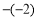 ,
,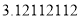 ….
….正数集合:{ …};
负数集合:{ …};
有理数集合:{ …};
无理数数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿
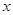 轴做如下移动,第一次点A向左移动3个单位长度到达点
轴做如下移动,第一次点A向左移动3个单位长度到达点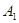 ,第二次将点
,第二次将点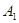 向右移动6个单位长度到达点
向右移动6个单位长度到达点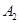 ,第三次将点
,第三次将点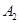 向左移动9个单位长度到达点
向左移动9个单位长度到达点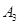 ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第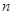 次移动到点
次移动到点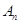 ,如果点
,如果点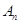 与原点的距离不小于20,那么
与原点的距离不小于20,那么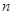 的最小值是 .
的最小值是 .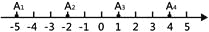
相关试题

