搜索
【题目】把下列各数填入它所属的集合内：将下列各数填入相应的括号内：
，
，
，
，
，
，
…．
正数集合：{ …}；
负数集合：{ …}；
有理数集合：{ …}；
无理数数集合：{ …}．
参考答案：
【答案】正数集合：{ 
,(2), 
,
…}；
有理数集合：{2.5, ,0,|3|,(2),…}；
分数集合：{2.5, ,…}；
非负整数集合：{0,(2),…}.
【解析】
利用正数，有理数，分数，以及非负整数定义判断即可．
正数：比0大的数叫正数；
有理数：有理数为整数（正整数、0、负整数）和分数的统称；
分数：分数是一个整数a和一个正整数b的不等于整数的比；
非负整数：不是负数的整数.
正数集合：{ ,(2), ,…}；
有理数集合：{2.5, ,0,|3|,(2),…}；
分数集合：{2.5, ,…}；
非负整数集合：{0,(2),…}.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，|a|表示a到原点的距离，这是绝对值的几何意义．进一步地，数轴上两个点A、B，分别用a、b表示，那么AB=|a－b|．（思考一下，为什么？），利用此结论，回答以下问题：
（1）数轴上表示2和5的两点之间的距离是_____．数轴上表示－2和－5的两点之间的距离___．数轴上表示1和－3的两点之间的距离是_____；
（2）数轴上表示x和－1的两点A、B之间的距离是___________；
如果|AB|=2，x的值为_____；
（3）说出|x+1|+|x+2|表示几何的意义_，该代数式的最小值是：_____；
（4）求|x－1|+|x－2|+|x－3|+．．．+|x－2019|的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上，A1、P两点表示的数分别为1、3，A1、A2关于O对称，A2、A3关于点P对称，A3、A4关于点O对称，A4、A5关于点P对称…依次规律，则点A15表示的数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】C，D两城蔬菜紧缺，A，B两城决定支援，A城有蔬菜20吨，B城有蔬菜40吨，C城需要蔬菜16吨，D城需要蔬菜44吨，已知A到C，D的运输费用分别为200元/吨，220元/吨，B到C，D的运输费用分别为300元/吨，340元/吨，规定A向C城运的吨数不小于B向C城运的吨数，设A城向C城运x吨，请回答下列问题：
（1）根据题意条件，填写下列表格：
（2）设总费用为y（元），求出y（元）与x（吨）的函数关系式，并写出x的取值范围；
（3）怎样调运货物能使总费用最少？最少费用是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．
（1）求证：四边形BFEP为菱形；
（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上，点A表示1，现将点A沿
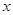轴做如下移动，第一次点A向左移动3个单位长度到达点
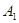，第二次将点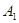向右移动6个单位长度到达点
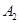，第三次将点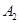向左移动9个单位长度到达点
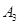，按照这种移动规律移动下去，第
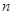次移动到点
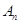，如果点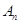与原点的距离不小于20，那么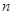的最小值是 ．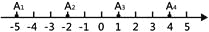
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=﹣x+1与x轴，y轴分别交于B，A两点，动点P在线段AB上移动，以P为顶点作∠OPQ=45°交x轴于点Q．
（1）求点A和点B的坐标；
（2）比较∠AOP与∠BPQ的大小，说明理由．
（3）是否存在点P，使得△OPQ是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
相关试题
