【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接DE并延长至点F,使EF=DE,连接AF、DC.求证:四边形ADCF是菱形. 
参考答案:
【答案】证明:∵点E是边AC的中点, ∴AE=EC.
又∵EF=DE,
∴四边形ADCF是平行四边形.
又∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC.
又∵∠ACB=90°,
∴∠AED=90°.
∴AC⊥DF.
∴四边形ADCF是菱形.
【解析】先证明四边形ADCF是平行四边形,再证明DE是△ABC的中位线,得出DE∥BC,证出AC⊥DF,即可得出结论
【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识,掌握直角三角形斜边上的中线等于斜边的一半,以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习过反比例函数y=
 的图象和性质,请回顾研究它的过程,对函数y=
的图象和性质,请回顾研究它的过程,对函数y=  进行探索.下列结论:
进行探索.下列结论:
①图象在第一、二象限,②图象在第一、三象限,
③图象关于y轴对称,④图象关于原点对称,
⑤当x>0时,y随x增大而增大;当x<0时,y随x增大而增大,
⑥当x>0时,y随x增大而减小;当x<0时,y随x增大而增大,
是函数y= 的性质及它的图象特征的是: . (填写所有正确答案的序号)
的性质及它的图象特征的是: . (填写所有正确答案的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,CA=4,CB=3.
 与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 .
与CA延长线、AB、CB延长线相切,切点分别为E、D、F,则该弧所在圆的半径为 . 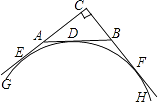
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为x厘米/秒,则当△BPD与△CQP全等时,x的值为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
-
科目: 来源: 题型:
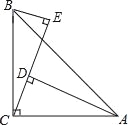
查看答案和解析>>【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE≌△CAD;
(2)若AD=25cm,BE=8cm,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】脸谱是中国戏曲男演员脸部的彩色化妆.这种脸部化妆主要用于净(花脸)和丑(小丑),表现人物的性格和特征.现有四张脸谱,如图所示:有两张相同的表现忠勇侠义的净角姜维,有一张表现直爽刚毅的净角包拯,有一张表现阴险奸诈的丑角夏侯婴.

(1)随机抽取一张,获得一张净角脸谱的概率是;
(2)随机抽取两张,求获得一张姜维脸谱和一张包拯脸谱的概率.
相关试题

