【题目】先化简,再求值:(1)(2x2+x﹣1)﹣[4x2+(5﹣x2+x)],其中x=﹣3.
(2)已知A=5x2﹣2xy﹣2y2,B=x2﹣2xy﹣y2,其中x=![]() ,y=﹣
,y=﹣![]() ,求
,求![]() A﹣B的值.
A﹣B的值.
参考答案:
【答案】(1)﹣x2﹣6,﹣15;(2)![]() x2+xy,0.
x2+xy,0.
【解析】
(1)先去括号,再合并同类项化简原式,再将x的值代入计算可得;
(2)将A、B所代表的多项式代入![]() A-B列出算式,再去括号、合并同类项化简原式,最后将x、y的值代入计算可得.
A-B列出算式,再去括号、合并同类项化简原式,最后将x、y的值代入计算可得.
(1)原式=2x2+x-1-4x2-(5-x2+x)
=2x2+x-1-4x2-5+x2-x
=-x2-6,
当x=-3时,
原式=-(-3)2-6
=-9-6
=-15;
(2)![]() A-B
A-B
=![]() (5x2-2xy-2y2)-(x2-2xy-y2)
(5x2-2xy-2y2)-(x2-2xy-y2)
=![]() x2-xy-y2-x2+2xy+y2
x2-xy-y2-x2+2xy+y2
=![]() x2+xy,
x2+xy,
当x=![]() 、y=-
、y=-![]() 时,
时,
原式=![]() ×
×![]() -
-![]() =
=![]() -
-![]() =0.
=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C) 记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)20+(﹣14)﹣(﹣18)﹣13; (2)﹣2
 ;
;(3)(﹣7)×(﹣5)﹣90÷(﹣15) (4)-120×
 +(-7)×
+(-7)× +37×
+37×
(5)﹣14﹣(1﹣0.5)×
 ×[2-(-3)2].
×[2-(-3)2]. -
科目: 来源: 题型:
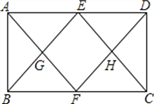
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三一班五个劳动竞赛小组一天植树的棵数是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 12 B. 10 C. 9 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读资料:
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB=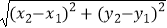 .
.
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.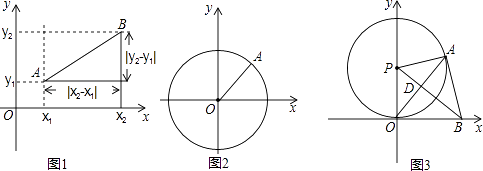
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是长方体纸盒的平面展开图,设 AB=x cm,若 AD =4x cm,AN=3x cm.
(1)求长方形 DEFG 的周长与长方形 ABMN 的周长(用字母 x 进行表示);
(2)若长方形 DEFG 的周长比长方形 ABMN 的周长少 8cm,求 x 的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.

相关试题

