【题目】初三一班五个劳动竞赛小组一天植树的棵数是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 12 B. 10 C. 9 D. 8
参考答案:
【答案】B
【解析】分析: 众数可能是10,也可能是12或8,因此应分众数是10或者众数是12,或者众数是8三种情况进行讨论.
详解: 当众数是10时,
∵众数与平均数相等,
∴![]() (10+10+12+x+8)=10,解得x=10.
(10+10+12+x+8)=10,解得x=10.
这组数据为:8,10,10,10,12,
∴中位数为10;
当众数是12时,∵众数与平均数相等,
∴![]() (10+10+12+x+8)=12,此题解出x=20,故不可能;
(10+10+12+x+8)=12,此题解出x=20,故不可能;
当众数是8时,∵众数与平均数相等,
∴![]() (10+10+12+x+8)=8,此题解出x=0,故不可能.
(10+10+12+x+8)=8,此题解出x=0,故不可能.
所以这组数据中的中位数是10.
故选B.
点睛: 本题考查了众数、平均数、中位数的求法及分类讨论的数学思想,正确运用分类讨论的思想是解答本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)20+(﹣14)﹣(﹣18)﹣13; (2)﹣2
 ;
;(3)(﹣7)×(﹣5)﹣90÷(﹣15) (4)-120×
 +(-7)×
+(-7)× +37×
+37×
(5)﹣14﹣(1﹣0.5)×
 ×[2-(-3)2].
×[2-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
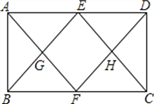
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(1)(2x2+x﹣1)﹣[4x2+(5﹣x2+x)],其中x=﹣3.
(2)已知A=5x2﹣2xy﹣2y2,B=x2﹣2xy﹣y2,其中x=
 ,y=﹣
,y=﹣ ,求
,求 A﹣B的值.
A﹣B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读资料:
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB=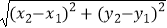 .
.
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.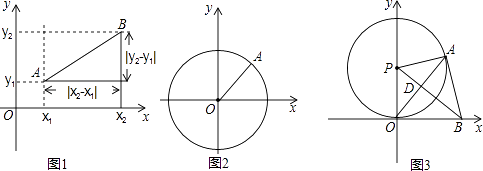
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是长方体纸盒的平面展开图,设 AB=x cm,若 AD =4x cm,AN=3x cm.
(1)求长方形 DEFG 的周长与长方形 ABMN 的周长(用字母 x 进行表示);
(2)若长方形 DEFG 的周长比长方形 ABMN 的周长少 8cm,求 x 的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚为班级购买了一、二、三等奖的奖品,已知一等奖奖品6元,二等奖奖品4元,三等奖奖品2元,其中获奖人数的分配情况如图,则小刚购买奖品费用的平均数和众数分别为( )%

A. 2元,3元 B. 2.5元,2.5元 C. 3元,2元 D. 3元,3元
相关试题

