【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤
;⑤![]() .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
参考答案:
【答案】①②③⑤
【解析】
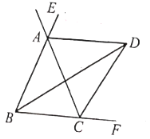
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ACB+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°-(∠DAC+∠ACD)
=180°-![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°-![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°-![]() (180°+∠ABC)
(180°+∠ABC)
=90°-![]() ∠ABC,∴③正确;
∠ABC,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-![]() ∠ABC,
∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵BD平分∠ABC,
∴∠CBD=∠CBD=![]() ∠ABC,
∠ABC,
∵CD平分∠ACF,
∴∠DCF=![]() ∠ACF,
∠ACF,
∴∠DCF-∠CBD=![]() ∠ACF-
∠ACF-![]() ∠ABC
∠ABC
∵∠BAC=∠ACF-∠ABC
∠BDC=∠DCF-∠CBD
∴∠BDC=![]() ∠BAC,⑤正确.
∠BAC,⑤正确.
故答案为:①②③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△AB C沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
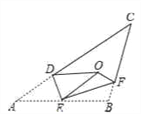
A. 40° B. 41° C. 42° D. 43°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α是锐角,且点A(
 ,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
A.a<b<c
B.a<c<b
C.b<c<a
D.c<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A6B6C6的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】画图计算:
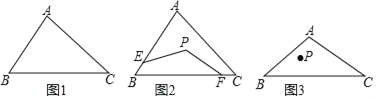
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为______.
相关试题

