【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A6B6C6的边长为 . 
参考答案:
【答案】![]()
【解析】解:作A2D1⊥A1B1于D1,A3D2⊥A2B2于D2,如图,
∵△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,
∴∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,
,
∴cos∠A2B1D1=cos30°= ![]() =
= ![]() ,
,
∴A2B1= ![]() ,
,
∵A2B1=B1B2,
∴A2B2= ![]() ,
,
同理可得∠A3B2D2=30°,B2D2= ![]() A2B2=
A2B2= ![]() ×
× ![]() =
= ![]() ,
,
∴cos∠A3B2D2=cos30°= ![]() =
= ![]() ,
,
∴A3B2= ![]() ,
,
∵A3B2=B2B3,
∴A3B3= ![]() =(
=( ![]() )2,
)2,
同理可得A4B4=( ![]() )3,
)3,
A5B5=( ![]() )4.A6B6C=(
)4.A6B6C=( ![]() )5=
)5= ![]() ,
,
故答案为 ![]() .
.
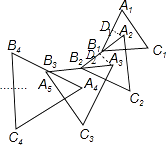
作A2D1⊥A1B1于D1,A3D2⊥A2B2于D2,根据等边三角形的中心的性质得∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,利用余弦的定义得cos∠A2B1D1=cos30°=
,利用余弦的定义得cos∠A2B1D1=cos30°= ![]() =
= ![]() ,可计算出A2B1=
,可计算出A2B1= ![]() ,由A2B1=B1B2得到A2B2=
,由A2B1=B1B2得到A2B2= ![]() ,用同样的方法可计算出A3B3=(
,用同样的方法可计算出A3B3=( ![]() )2,特殊的结论.
)2,特殊的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α是锐角,且点A(
 ,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
A.a<b<c
B.a<c<b
C.b<c<a
D.c<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
,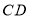 分别平分
分别平分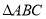 的外角
的外角 ,内角
,内角 ,外角
,外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 平分
平分 ;⑤
;⑤ .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)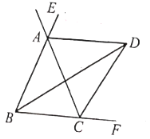
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图计算:
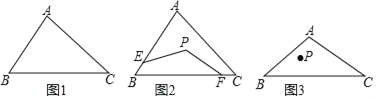
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
相关试题

