【题目】画图计算:
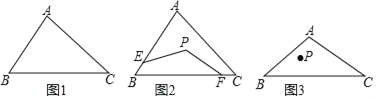
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为______.
参考答案:
【答案】(1)见解析;(2)①∠EPF=120°;②BP=![]() ;(3)7
;(3)7![]() .
.
【解析】
(1)作∠ABC的平分线BM,线段BC的垂直平分线EF,直线EF交射线BM于点P,点P即为所求;
(2)①由Rt△PME≌Rt△PNF(HL),推出∠EPM=∠FPN,推出∠EPF=∠MPN,即可解决问题;
②由Rt△PMB≌Rt△PNB(HL),推出BM=BN,由Rt△PME≌Rt△PNF(HL),推出EM=FN,推出BE+BF=BM-EM+BN+NF=2BN=10,推出BN=NM=5,再利用勾股定理即可解决问题;
(3)分别作点P关于边AB、BC的对称点E、F,连接EF,分别与边AB、BC交于点M、N,连接PM、PN.则线段EF的长度即为△PMN的周长的最小值;
解:(1)如图,点P即为所求;
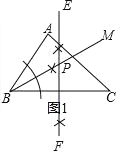
(2)①连接BP,作PM⊥AB于M,PN⊥BC于N.
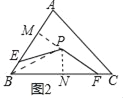
∵BP平分∠ABC,PM⊥AB,PN⊥BC,
∴PM=PN,
∵PE=PF,∠PME=∠PNF=90°,
∴Rt△PME≌Rt△PNF(HL),
∴∠EPM=∠FPN,
∴∠EPF=∠MPN,
∵∠MPN=360°﹣90°﹣90°﹣60°=120°,
∴∠EPF=120°.
②∵PB=PB,PM=PN,∠PMB=∠PFB=90°
∴Rt△PMB≌Rt△PNB(HL),
∴BM=BN,
∵Rt△PME≌Rt△PNF(HL),
∴EM=FN,
∴BE+BF=BM﹣EM+BN+NF=2BN=10,
∴BN=NM=5,
∵BE=2,PE=5,
∴EM=3,PM=![]() =4,
=4,
∴BP=![]() =
=![]() .
.
(3)分别作点P关于边AB、BC的对称点E、F,连接EF,分别与边AB、BC交于点M、N,连接PM、PN.则线段EF的长度即为△PMN的周长的最小值.
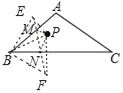
∵点E与点P关于AB对称,点F与点P关于BC对称,
∴∠EBA=∠PBA,∠FBC=∠PBC,BE=BF=BP=7.
∴EF=![]() BE=7
BE=7![]()
∴△PMN周长的最小值为7![]() .
.
故答案为7![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
,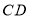 分别平分
分别平分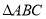 的外角
的外角 ,内角
,内角 ,外角
,外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③ ;④
;④ 平分
平分 ;⑤
;⑤ .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)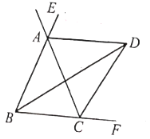
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A6B6C6的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
小淇同学作法如下:
(1)在直线l上任意取一点C,连接AC;
(2)作AC的中点O;
(3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示;
(4)作直线AB.
则直线AB就是所要作图形.
你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.

相关试题

