搜索
【题目】如图，方格纸中每个小正方形的边长均为1，建立如图所示的直角坐标系，已知两点A（0，2），B（4，1）
（1）请在x轴上画出一点P，使得PA+PB的值最小；
（2）请直接写出：点P的坐标 ；PA+PB的最小值为 ．
参考答案：
【答案】（1）详见解析；（2）P点坐标为（
，0），PA+PB的最小值为5．
【解析】
（1）作A点关于x轴的对称点A′，连结BA′交x轴于P点，利用对称的性质得到PA＝PA′，则PA+PB＝PA′+PB＝BA′，于是利用两点之间线段最短可判断P点满足条件；
（2）先写出点A′的坐标为（0，﹣2），再利用待定系数法求出直线BA′的解析式为y＝
x﹣2，然后解方程x﹣2＝0得P点坐标，然后利用两点间的距离公式求出BA′即可．
解：（1）如图，点P为所作；
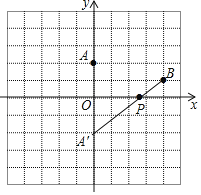
（2）A点关于x轴对称的点A′的坐标为（0，﹣2），
设直线BA′的解析式为y＝kx+b，
把A′（0，﹣2），B（4，1）得
，解得，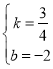
∴直线BA′的解析式为y＝x﹣2，
当y＝0时，x﹣2＝0，解得x＝，
∴P点坐标为（，0），
PA+PB的最小值＝
，
故答案为：（，0），5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的方程rx2+（r+2）x+r﹣1=0有根只有整数根的一切有理数r的值有（ ）个．
A. 1 B. 2 C. 3 D. 不能确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠ACB＝90°，BC＝a，AC＝b，AB＝c．将Rt△ABC绕点O依次旋转90°、180°和270°，构成的图形如图所示．该图是我国古代数学家赵爽制作的“勾股圆方图”，也被称作“赵爽弦图”，它是我国最早对勾股定理证明的记载，也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据．
（1）请利用这个图形证明勾股定理；
（2）请利用这个图形说明a2＋b2≥2ab，并说明等号成立的条件；
（3）请根据（2）的结论解决下面的问题：长为x，宽为y的长方形，其周长为8，求当x，y取何值时，该长方形的面积最大？最大面积是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此规律，将△OAB进行n次变换，得到△OAnBn。推测An的坐标是___________，Bn的坐标是___________。（ ）
A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)
-
科目： 来源： 题型：
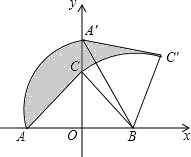
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，根据要求回答下列问题：
（1）点A关于y轴对称点A′的坐标是 ；点B关于y轴对称点B′的坐标是
（2）作出△ABC关于y轴对称的图形△A′B′C′（不要求写作法）
（3）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知动点A在函数y=
（x＞0）的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点P，Q，当QE：DP=9：25时，图中的阴影部分的面积等于___．
相关试题
