【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() -8.
-8.
【解析】试题分析:(1)连接AD、OD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,于是可判断OD为△ABC的中位线,所以OD∥AC,则DF⊥OD,然后根据切线的判定定理可得DF是⊙O的切线;
(2)利用S阴影=S扇形AOE-S△AOE进而求出答案.
试题解析:(1)连接AD,OD.
∵AB是直径,
∴∠ADB=90°,∴AD⊥BC.
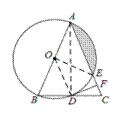
∵AB=AC ,
∴D是BC的中点.
∵O是AB的中点,
∴OD//AC.
∴∠ODF+∠DFA=180°
∵DF⊥AC,∴∠DFA=90°.
∴∠ODF=90°. ∴OD⊥DF
∴DF是⊙O的切线.
(2)连接OE
∵∠ADB=∠ADC=90°,∠DFC=∠DFA=90°,
∴∠DAC=∠CDF=22.5°
∵AB=AC,D是BC中点,
∴∠BAC=2∠DAC=2×22.5°=45°.
∵OA=OE,
∴∠OEA=∠BAC=45°.
∴∠AOE=90° .
∵AE=4![]() ,
,
∴OA=OE=4.
S阴影=S扇形AOE-S△AOE=4π-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, 是
是 边上一点,在
边上一点,在 上取一点
上取一点 ,使
,使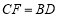 ,在
,在 边上取一点
边上取一点 ,使
,使 ,则
,则 的度数为( )
的度数为( )
A.
 B.
B.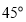 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题:

(1)以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1,画出△CA1B1;
(2)作出△ABC关于点A成中心对称的△AB2C2;
(3)设AC2与y轴交于点D,则△B1DC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生对各种球类运动的喜爱程度,小明采取随机抽样的方法对他所在学校的部分学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一种项目),对调查结果进行统计后,绘制了下面的统计图(1)和图(2).


(1)此次被调查的学生共有___人,m=_____;
(2)求喜欢“乒乓球”的学生的人数,并将条形统计图补充完整;
(3)若该校有2000名学生,估计全校喜欢“足球”的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.

(1)判断△DEF的形状,并说明理由;
(2)若点F是BC的中点,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.


(1)如图1,求证:OH=
 AD,OH⊥AD;
AD,OH⊥AD;(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
相关试题

