【题目】为了解学生对各种球类运动的喜爱程度,小明采取随机抽样的方法对他所在学校的部分学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一种项目),对调查结果进行统计后,绘制了下面的统计图(1)和图(2).


(1)此次被调查的学生共有___人,m=_____;
(2)求喜欢“乒乓球”的学生的人数,并将条形统计图补充完整;
(3)若该校有2000名学生,估计全校喜欢“足球”的学生大约有多少人?
参考答案:
【答案】(1)50,20;(2)5人,图见解析;(3)400人
【解析】
(1)利用喜欢篮球的人数与所占总体的百分比可得总人数,利用喜欢足球的人数占总体的百分比可得![]() 的值,
的值,
(2)利用总人数与各部分的人数差可得答案,依据答案补全条形统计图即可,
(3)利用样本中喜欢足球所占的百分比乘以总人数即可得到答案.
解:(1)由![]() (人),所以被调查的学生共有50人,
(人),所以被调查的学生共有50人,
![]() 所以
所以![]()
故答案为:50,20
(2)喜欢乒乓球的有:50-20-10-15=5(人)
如图所示:

(3)喜欢足球的大约有:2000![]() =400(人)
=400(人)
答:估计全校喜欢“足球”的学生人数为400人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, 是
是 边上一点,在
边上一点,在 上取一点
上取一点 ,使
,使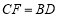 ,在
,在 边上取一点
边上取一点 ,使
,使 ,则
,则 的度数为( )
的度数为( )
A.
 B.
B.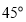 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题:

(1)以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1,画出△CA1B1;
(2)作出△ABC关于点A成中心对称的△AB2C2;
(3)设AC2与y轴交于点D,则△B1DC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=1,BC=2,点E在AD上,点F在BC边上,FE平分∠DFB.

(1)判断△DEF的形状,并说明理由;
(2)若点F是BC的中点,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.


(1)如图1,求证:OH=
 AD,OH⊥AD;
AD,OH⊥AD;(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
相关试题

