【题目】(1)尺规作图:如图1,请在x轴上作出表示(![]() ,0)的点(保留清晰作图痕迹,不写作法).
,0)的点(保留清晰作图痕迹,不写作法).
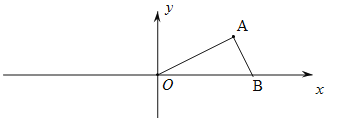
(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
参考答案:
【答案】(1)答案见解析;(2)(5,0);(3)(8,0),(2.5,0),(![]() ,0),(-
,0),(-![]() ,0).
,0).
【解析】
(1)过2作y轴的垂线,过-4作x轴的垂线,交于点B,连接OB,以O为圆心,OB为半径作弧交x轴负半轴于点A,则点A就是所求的点.
(2)用待定系数法求出直线OA的解析式.设直线AB为y=ax+b,由BA⊥OA,得到a=-2,把A(4,2)代入得到b的值,从而得到直线AB的解析式,令y=0,求得x的值,即可得到结论.
(3)分三种情况讨论:①以O为圆心,OA为半径作圆O交x轴于点C1,C2;②以A为圆心,OA为半径作圆A交x轴于点O,C3;③作OA的垂直平分线交x轴于点C4.分别求出点C的坐标即可.
(1)如图,过2作y轴的垂线,过-4作x轴的垂线,交于点B,连接OB,以O为圆心,OB为半径作弧交x轴负半轴于点A,则OA=OB=![]() ,∴A(
,∴A(![]() ,0).
,0).
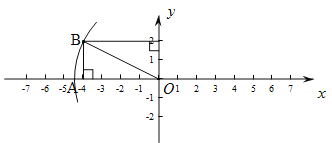
(2)设直线OA为y=kx,把A(4,2)代入得:2=4k,解得:k=![]() ,∴直线OA的解析式为y=
,∴直线OA的解析式为y=![]() x.设直线AB为y=ax+b.
x.设直线AB为y=ax+b.
∵BA⊥OA,则a=-2,∴直线AB为y=-2x+b,把A(4,2)代入得:2=-2×4+b,解得:b=10,∴y=-2x+10.在y=-2x+10中,令y=0,解得:x=5,∴B(5,0).
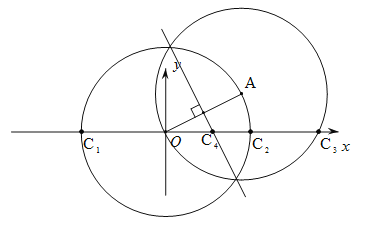
(3)分三种情况讨论:
①以O为圆心,OA为半径作圆O交x轴于点C1,C2,则OC1=OC2=OA=![]() ,∴C1(
,∴C1(![]() ,0),C2(
,0),C2(![]() ,0);
,0);
②以A为圆心,OA为半径作圆A交x轴于点O,C3,则OC3=2×4=8,∴C3(8,0);
③作OA的垂直平分线交x轴于点C4,则OC4=AC4.设C4(x,0),则![]() ,解得:x=2.5,∴C4(2.5,0).
,解得:x=2.5,∴C4(2.5,0).
综上所述:点C的坐标为(8,0)或(2.5,0)或(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.
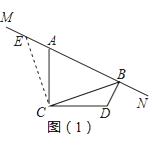
(1)问题发现
如图(1),过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为 , BD、AB、CB之间的数量关系为 .
(2)拓展探究
当MN绕点A旋转到如图(2)位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并给予证明.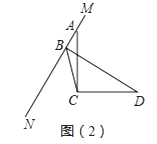
(3)解决问题
当MN绕点A旋转到如图(3)位置时(点C、D在直线MN两侧),若此时∠BCD=30°,BD=2时,CB= .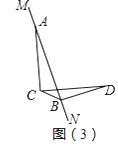
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.

(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是___;
(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,请结合数据简要分析该校学生对剪纸课程的兴趣情况.
-
科目: 来源: 题型:
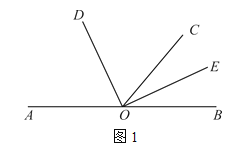
查看答案和解析>>【题目】已知,O为直线AB上一点,∠DOE=90°.
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
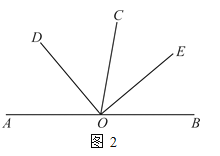
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
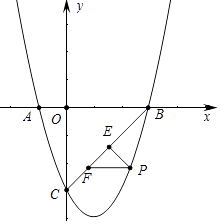
(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点P,过点p作PE⊥BC于点E,作PF平行于x轴交直线BC于点F,求△PEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,
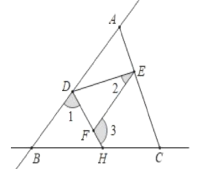
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
相关试题

